Filter
Top Products
3.6. H
2
AND H
∞
ANALYSIS AND SYNTHESIS 105
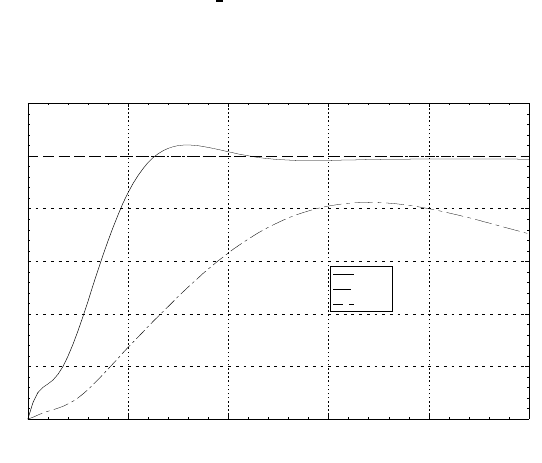
g3 = ctrlplot(step,g3,{line
style=2});
g3 = plot(g3,{title="Step responses",...
legend=["Kinf";"K2";"input"]})?
24680 10
0.2
0.4
0.6
0.8
1
0
1.2
Step responses
Kinf
K2
input
3.6.2 System Norm Calculations
Functions are provided for calculating the H
2
and H
∞
norms of Dynamic Systems. In
the H
2
case, this involves the solution of a Lyapunov equation. A bisection method,
involving the calculation of eigenvalues of a scaled Hamiltonian matrix, is required for
the H
∞
norm calculation.
The Xµ function for the two norm calculation is called h2norm. The syntax and
operation are self explanatory.
The calculation of the H
∞
norm involves the iterative solution of a Riccati equation.
The technique is a generalization of the the theoretical result given in Lemma 2 in
Section 2.3.3. As a result, a tolerance can be specified, and the calculation gives upper
and lower bounds. The function is hinfnorm. The syntax is illustrated below.
[out,omega] = hinfnorm(system,tol)