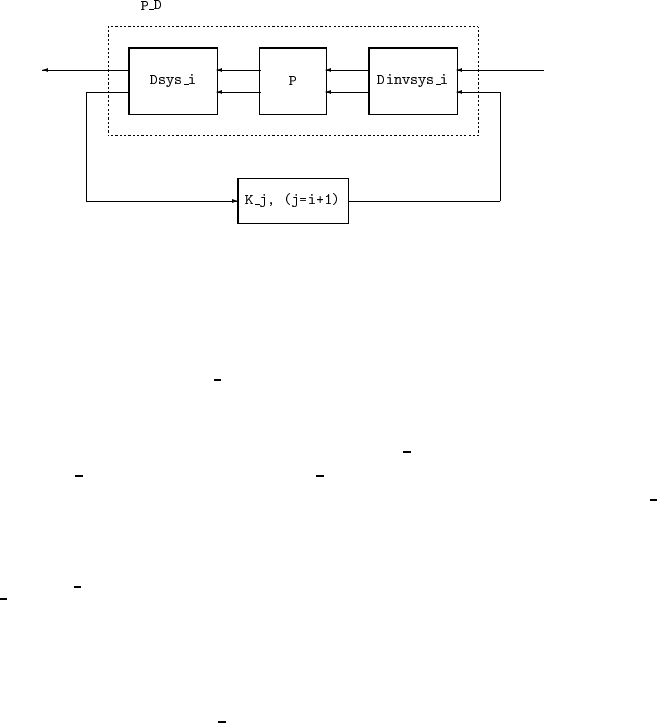
112 CHAPTER 3. FUNCTIONAL DESCRIPTION OF Xµ
Figure 3.9: H
∞
controller design. Step 9 in the enumerated procedure
There is actually another possibility at step 5; numerical problems cause the iteration to
diverge. As γ approaches its optimal value, the numerical properties of the calculation
deteriorate. This may lead to mu(G
i) increasing as i is increased. This problem is
observed more often in systems with very lightly damped modes.
A comparison of Figures 3.8 and 3.9 will show that Dsys
i is not quite a rational
approximation to D
i. The reason is that Dsys i has as inputs, the lower outputs of P.
These are actually passed through an identity for the design of the next controller: K
j
(with j = i+1). In other words,
Dsys
i ≈
D
i 0
0 I
.
This identity is of dimension nmeas × nmeas and is the reason that nmeas and nctrls
must be passed to the musynfit function. Do not confuse this identity with that
corresponding to the last block in D
i.
3.7.3 Fitting D Scales
The XµD-scale fitting function is musynfit; the syntax is as follows.
[Dsys,Dinvsys] = musynfit(Dmagdata,blk,nmeas,nctrls,weight)


















