128 CHAPTER 4. DEMONSTRATION EXAMPLES
δv Perturbations along the velocity vector.
α Angle of attack. I.e. angle between the velocity vector and the aircraft’s longitudinal
axis.
q Rate-of-change of aircraft attitude angle.
θ Aircraft attitude angle.
Control can be exerted via the elevon and canard, denoted by δ
e
and δ
c
respectively.
The angle of attack (α) and attitude angle (θ) are available as direct measurements.
A weighted output disturbance rejection problem will be considered. This problem also
encompasses other maneuvering objectives. The closed-loop perturbation model of the
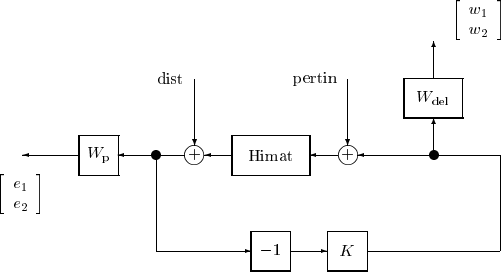
vehicle is illustrated in Figure 4.1.
Figure 4.1: Himat open-loop perturbation model
Note that W
p
, W
del
, Himat and K are each two-input, two-output systems. Similarly,
the inputs dist and pertin are two element vector signals. The desired result is the
four-input, four-output system, denoted by clp, and shown in Figure 4.2. This is used in
the design example given below.
4.1.2 State-space Model of Himat
The state space description of the Himat plane is given below. The states of the plant
model are: forward speed (v), angle-of-attack (α), pitch rate (q) and pitch angle (θ).