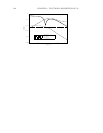
4.1. THE HIMAT EXAMPLE 133
sysn = ["himat";"wdel";"wp"]
in = ["pert(2)";"dist(2)";"control(2)"]
out = ["wdel";"wp";"himat + dist"]
inter = ["control + pert"; "control"; "himat + dist"]
himat
ic = sysic(sysn,in,out,inter,himat,wdel,wp)
comment himat
ic "Himat design interconnection structure"
4.1.4 H
∞
Design
The next step is to design an H
∞
control law for Himat. The function hinfsyn designs
an H
∞
control law based on the interconnection structure provided. hinfsyn requires
the design interconnection structure, number of measurements, number of controls and
single gamma or bisection bounds on γ.
Optional input arguments are the tolerance for terminating the γ iteration (tol), an
epsilon for Hamiltonian jω-axis eigenvalues (epr) and the epsilon for the Riccati
solution positive definite tests (epp). Two Riccati solution methods are provided:
eigenvalue or Schur (default) decomposition. hinfsyn returns the control law, k and the
gamma value achieved, gf1.
In this example, the system interconnection structure is himat
ic, with 2 measurements,
2 controls, a γ lower bisection bound of 0.8, a γ upper bisection bound of 6, a tolerance
on the γ iteration of 0.05, and we’ll use the eigenvalue decomposition method to solve
the Riccati equations. The default values of epr (0.5*sqrt(eps))andepp (1e-6) will be
used for the epsilon tests.
gamma
bounds = [0.8;6.0]
nmeas = 2 # 2 measurements: attack angle & pitch
nctrls = 2 # 2 controls: elevon & canard
comment nmeas "number of controller measurements"
comment nctrls "number of controller outputs"
[k1,gf1] = hinfsyn(himat
ic,nmeas,nctrls,gamma bounds,{tol=0.05})
Test bounds: 0.8000 < gamma <= 6.0000