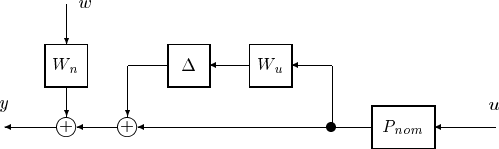
2.2. MODELING UNCERTAIN SYSTEMS 21
Figure 2.6: Example model: multiplicative output perturbation with weighted output
noise
References to a robust control model will imply a description of the form given in
Equation 2.8.
As a example, consider one of the most common perturbation model descriptions,
illustrated in Figure 2.6. This model represents a perturbed system with bounded noise
at the output.
The example model is given by,
y = W
n
w +(I+∆W
u
)P
nom
u.
The system W
n
is a frequency dependent weight on the noise signal, w. This allows us
to use a normalized representation for w. In other words the model includes the
assumption that w
∞
≤ 1. Similarly, we assume that ∆
∞
≤ 1andW
u
is a frequency
dependent weight which specifies the contribution of the perturbation at each frequency.
In a typical model W
n
will be small (assuming that the noise is small compared to the
nominal output) and W
u
will increase at high frequencies (to capture the likely case that
we know less about the model at higher frequencies). The LFT representation of this
model is,
y = F
u
(P,∆)
w
u
,
where
P =
00W
u
P
nom
IW
n
P
nom


















