EL-9650/9600c/9450/9400 Graphing Calculator
8-2
There may be differences in the results of calculations and graph plotting depending on the setting.
Return all settings to the default value and delete all data.
NotesStep & Key Operation
(When using EL-9650/9600c)
*Use either pen touch or cursor to operate.
Display
(When using EL-9650/9600c)
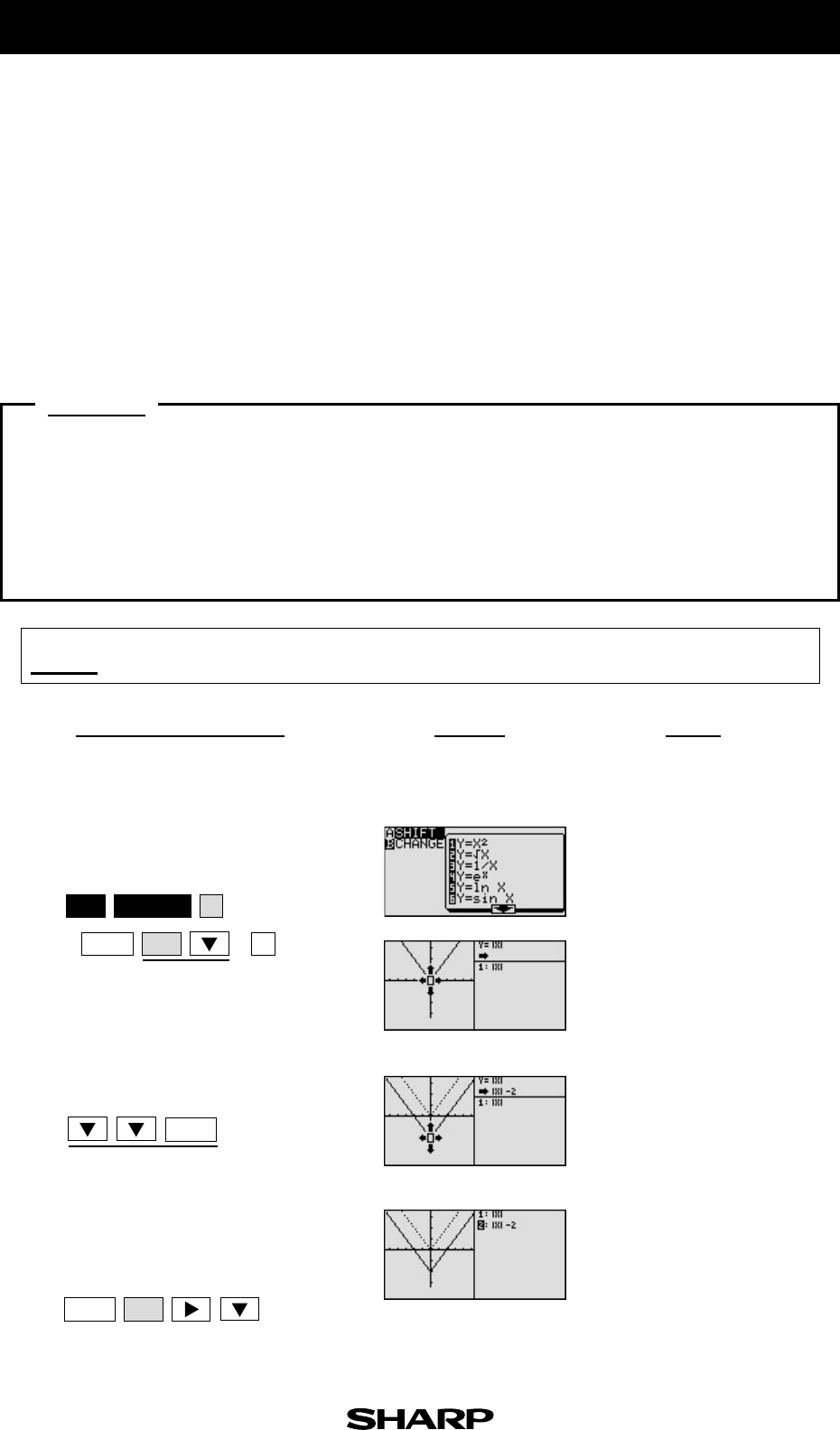
Shifting a graph of Absolute Value Functions
The absolute value of a real number x is defined by the following:
|x| = x if x
≥
0
-x if x
≤
0
If n is a positive number, there are two solutions to the equation |f (x)| = n because there
are exactly two numbers with the absolute value equal to n: n and -n. The existence of two
distinct solutions is clear when the equation is solved graphically.
An absolute value function can be presented as y = a|x - h|+ k. The graph moves as the
changes of slope a, x-intercept h, and y-intercept k.
Move and change graphs of absolute value function y =|x| to check the relation
between the graphs and the values of coefficients.
Example
1. Move the graph y = |x| downward by 2 using the Shift feature.
2. Move the graph y = |x| to the right by 2 using the Shift feature.
3. Pinch the slope of y = |x| to 2 or minus using the Change feature.
1-2
y =|x|changes to y = |x|-2
Move the graph downward by 2.
1-1 Access the Shift feature.
Select y = |x|.
*
(
*
)
*
*
1-3
Save the new graph and look at the
relationship of the function and the
graph.
The graph of the equation that
is highlighted is shown by a
solid line. Notice that the y-
intercept k in the standard
form y = a|x - h|+ k takes
charge of vertical movement
of the graph.
2nd F
SHIFT/CHANGE
ENTER
ENTER
ENTER
ALPHA
ALPHA
A
8
Before
Starting


















