62 CHAPTER 6. IMPLEMENTATION IN CAML
6.4 Some predefined constants
HOL has a large number of constants predefined. The most basic of these are the
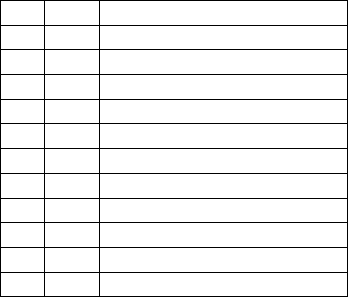
logical operators whose definitions were given in passing above. Here is a table
showing the conventional logical symbols, HOL’s ASCII approximation, and the
English reading. In the concrete syntax, they bind according to their order in the
above table, negation being strongest and the variable-binding operations weakest.
⊥ F Falsity
T Truth
¬ ~ Not
∧ /\ And
∨ \/ Or
⇒ ==> Implies
≡ = If and only if
∀ ! For all
∃ ? There exists
∃! ?! There exists a unique
ε @ Some . .. such that
λ \ The function taking .. .to
Readers are no doubt used to writing symbols like + rather than the word ‘plus’,
but may well find these analogous logical operations less familiar. However, it’s
worth spending some time getting accustomed to them, since they are needed to
understand most HOL terms. Here are a few examples:
• T says ‘truth holds’.
• F ==> p says ‘if falsity holds, so does any p’.
• !x. x > 0 = (?y. x = y + 1) says ‘for all x, x is greater than zero if and
only if there exists a y such that x = y + 1’.
• x >= y /\ u > v ==> x + u > y + v says ‘if x is greater than or equal to
y and u is greater than v, then x + u is greater than y + v’.
• p /\ q ==> q \/ r says ‘if p and q are true, then either q or r is true’.
• ~(p = ~p) says ‘it is always false that p holds if and only if p does not hold’.
• (m * n = 0) = (m = 0) \/ (n = 0) says ‘mn is zero if and only if either m
is zero or n is zero’.
• (\x. x + 1) 3 = 4 says that the function mapping any x to x + 1, when
applied to the argument 3, is equal to 4.
• (?!x. P x) ==> !a. P(a) = (a = @x. P x) says ‘if there is a unique x sat-
isfying P, then for all a, P holds of a if and only if a is equal to some canonical
x satisfying P’.
• !P. (!n. (!m. m < n ==> P m) ==> P n) ==> !n. P n expresses the prin-
ciple of complete mathematical induction, i.e. ‘for every predicate P over
numbers, if for each n, whenever P holds for each smaller m, then P holds
for n, then for every n, P holds’.


















