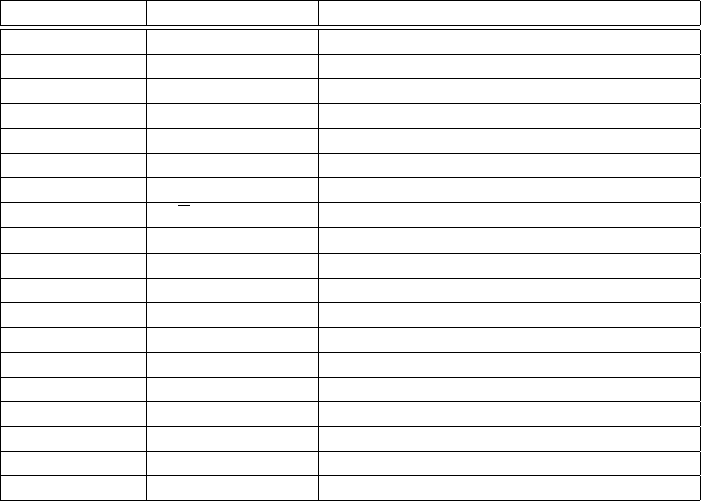
6.4. SOME PREDEFINED CONSTANTS 63
There are also a lot of constants defined in mathematical theories. Most of these
should look familiar, and in any case are summarized in a later chapter. However,
the following is a list of some of the less obvious ones, which may help the reader
follow some of the examples below.
HOL notation Standard symbol Meaning
SUC n n + 1 Successor of n
# (none) Natural map N → R or N → Z
--x −x Unary negation of x
inv(x) x
−1
Multiplicative inverse of x
abs(x) |x| Absolute value of x
m EXP n m
n
Natural m raised to natural power n
x pow n x
n
Real x raised to natural number power n
root n x
n
√
x Positive n
th
root of x
Sum(n,d) f Σ
n+d−1
i=n
f(i) Sum of d terms f(i) starting with f(n)
x IN s x ∈ s x is a member of set s
EMPTY ∅ The empty set
UNIV none Universe set for a type
x INSERT s {x} ∪ s Set s with element x
s DELETE x s − {x} Set s without element x
s UNION t s ∪ t Union of sets s and t
s INTER t s ∩ t Intersection of sets s and t
s DIFF t s − t Difference of sets s and t
UNIONS s
s Union of all members of s
INTERS s
s Intersection of all members of s
Formally, naturals, integers and reals are all different types, hence the use of a
mapping # between then. The usual arithmetic operations like + are overloaded,
meaning that they are used for addition of reals, integers, and natural numbers.
(The main exception is that EXP is used for natural numbers.) The next chapter
explains the translation from the usual symbols to different constants under the
surface.
