Chapter 2. SPECIFICATIONS
2 - 7
2) Integral Action (I Aaction)
(1) When a deviation(E) occurs between SV and PV, Integral action continuously adds the deviation to or
subtracts it from the MV in accordance time in order to eliminate the deviation
When a deviation is small it is not expected that the MV will be changed by P action but I action will
eliminate it.
Therefore, the offset which occurs in P action can be eliminated by I action.
(2) The period of the time from when the deviation has occurred in I action to when the MV of I action become
that of P action is called Integration time and represented as Ki.
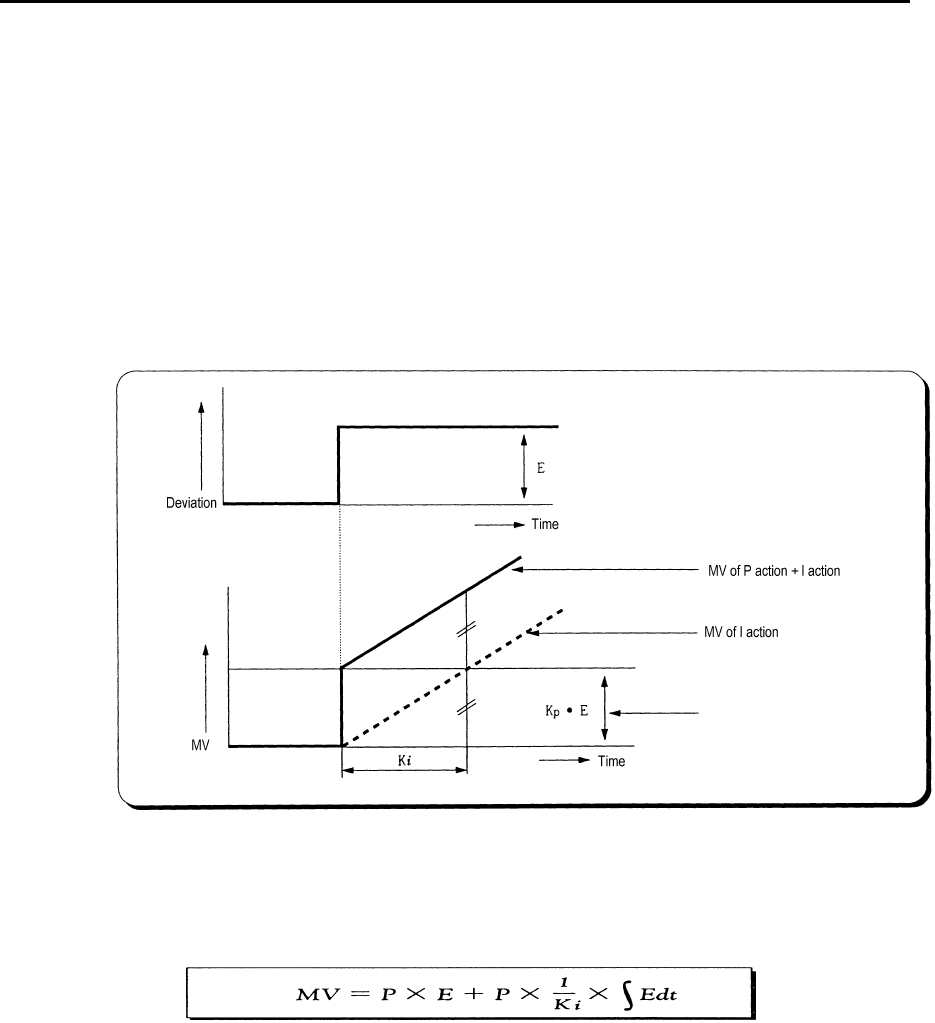
(3) Integral action when a given deviation has occurred is shown as the following Fig. 2.4.
[Fig. 2.4] Integral action at a constant deviation
(4) Expression of Integral Action is as follows:
As shown in the expression, Integral action can be made stronger or weaker by adjusting integration time
(Ki) in I action.
That is, the more the integration time (the longer the integration time) as shown in Fig. 2.5, the lesser the
quantity added to or subtracted from the MV and the longer the time needed for the PV to reach the SV.
As shown in Fig. 2.6, when the integration time given is short the PV will approach the SV in short time
since the quantity added or subtracted become increased. But, If the integration time is too short then
oscillations occurs, therefore, the proper P.I value is requested.
(5) Integral action is used in either PI action in which P action combines with I action or PID action in which P
and D actions combine with I action.
MV
MV of P action


















