169
Complex Samples Crosstabs
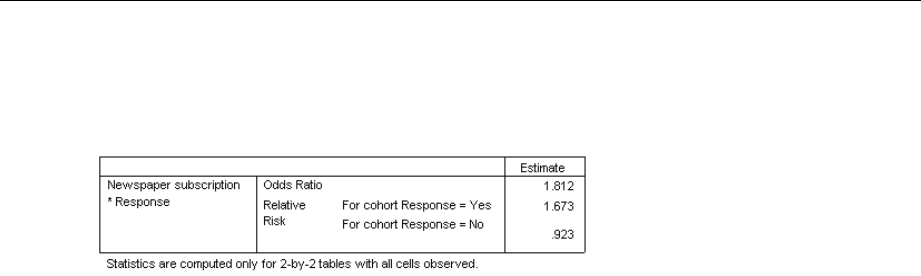
Risk Estimate
Figure 17-5
Risk estimate for newspaper subscription by response
The relative risk is a ratio of event probabilities. The relative risk of a response to the mailing
is the ratio of the probability that a newspaper subscriber responds to the probability that a
nonsubscriber r esponds. Thus, the estimate of the relative risk is simply 17.2%/10.3% = 1.673.
Likewise, the relative risk of nonresponse is the ratio of the probability that a subscriber does not
respond to the probability that a nonsubscriber does not respond. Your estimate of this relative
risk is 0.923. Given these results, you can estimate that a newspaper subscriber is 1.673 times as
likely to respond to the mailing as a nonsubscriber, or 0 .923 times as likely as a nonsubscriber
not to respond.
The odds ratio is a ratio of event odds. The odds of an event is the ratio of the probability that
the event occurs to the probability that the event does not occur. Thus, the estimate of the odds
that a newspaper subscriber responds to the mailing is 17.2%/82.8% = 0.208. Likewise, the
estimate of the odds that a nonsubscriber responds is 10.3%/89.7% = 0.115. The estimate of the
odds ratio is therefore 0.208/0.115 = 1.812 (note there is some rounding error in the intervening
steps). The odds ratio is also the ratio of the relative risk of responding to the relative risk of not
responding, or 1.673/0.923 = 1.812.
Odds Ratio versus Relative Risk
Since it is a ratio of ratios, the odds ratio is very difficult to interpret. T
he relative risk is easier
to interpret, so the odds ratio alone is not very helpful. However, there are certain commonly
occurring situations in which the estimate of the relative risk is not very good, and the odds ratio
can be used to approximate the relative risk of the event of interest. The o
dds ratio should be
used as an approximation of the relative risk of the event of interest when both of the following
conditions are met:
The probability of the event of interest is small (< 0.1) . This condition guarantees that the
odds ratio will make a good approximation to the relative risk. In this example, the event of
interest is a response to the mailing.
The design of the study is case control. This condition signals that th
e usual estimate of the
relative risk will likely not be good. A case-control study is retrospective, most often used
when the event of interest is unlikely or when the design of a prospective experiment is
impractical or unethical.
Neither condition is met in this example, since the overall proportion of respondents was 12.8%
and the design of the study was not case cont rol, so it’s safer to report 1.673 as the relative risk,
rather than the value of the odds ratio.
