121
Appendix
Using the Solver Function Effectively
The calculator uses Newton’s method to solve equations. (See page 52.)
Because of this, the solution it provides may differ from the true solution, or
an error message may be displayed for a soluble equation. This section
shows how you can obtain a more acceptable solution or make the equation
soluble in such cases.
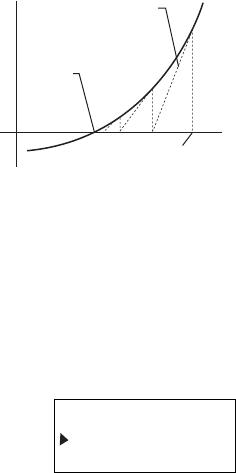
Newton’s method
Newton’s method is a successive
approximation technique that uses
tangential lines. The calculator chooses
an ‘approximate’ solution then calculates
and compares the right-hand and left-
hand sides of the equation. Based on the
result of this comparison, it chooses
another ‘approximate’ solution. It repeats
this process until there is hardly any
discrepancy between the right-hand and
left-hand sides of the equation.
‘Dead end’ approximations
When @ h is pressed for the first
time, the calculator takes the value that is stored in memory, or zero if no
value is stored, to be the initial expected value for the unknown variable and
tries to solve the equation. If it fails to find an acceptable solution using this
expected value, it tries again using up to nine more initial expected values
until a solution is found. If none of the values
lead by successive approximation toward an
acceptable solution — but rather to a ‘dead
end’ — the calculator will abort calculation and
display an error message.
Range of expected values
After the stored value (or zero) has been tried, new initial expected values
are selected according to the range of expected values for the equation.
(See ‘Changing the range of expected values’.) To choose which initial
expected values to try, the calculator divides the range into eight subranges
of equal width and tries each of the values at the edges of these subranges
in turn (starting with the lower limit of the range of expected values, a).
- ERROR 02 -
CALCULATION
Solution
Tangential lines
Initial value
y
x
y = f(x)
Newton’s method
Intersections of dotted lines with
the x-axis give successive
approximate solutions found using
Newton’s method.


















