EL-9650/9600c/9450/9400 Graphing Calculator
2-2
There may be differences in the results of calculations and graph plotting depending on the setting.
Return all settings to the default value and delete all data.
NotesStep & Key Operation
(When using EL-9650/9600c)
*Use either pen touch or cursor to operate.
Display
(When using EL-9650/9600c)
Shifting a Graph of Quadratic Equations
A quadratic equation of y in terms of x can be expressed by the standard form y = a (x - h)
2
+ k,
where a is the coefficient of the second degree term (y = a
x
2
+ bx + c) and (h, k) is the vertex
of the parabola formed by the quadratic equation. An equation where the largest exponent
on the independent variable x is 2 is considered a quadratic equation. In graphing quadratic
equations on the calculator, let the x-variable be represented by the horizontal axis and let y
be represented by the vertical axis. The relation of an equation and its graph can be seen by
moving the graph and checking the coefficients of the equation.
Move or pinch a graph of quadratic equation y = x
2
to verify the relation between
the coefficients of the equation and the graph.
Example
1. Shift the graph y = x
2
upward by 2.
2. Shift the graph y = x
2
to the right by 3.
3. Pinch the slope of the graph y = x
2
.
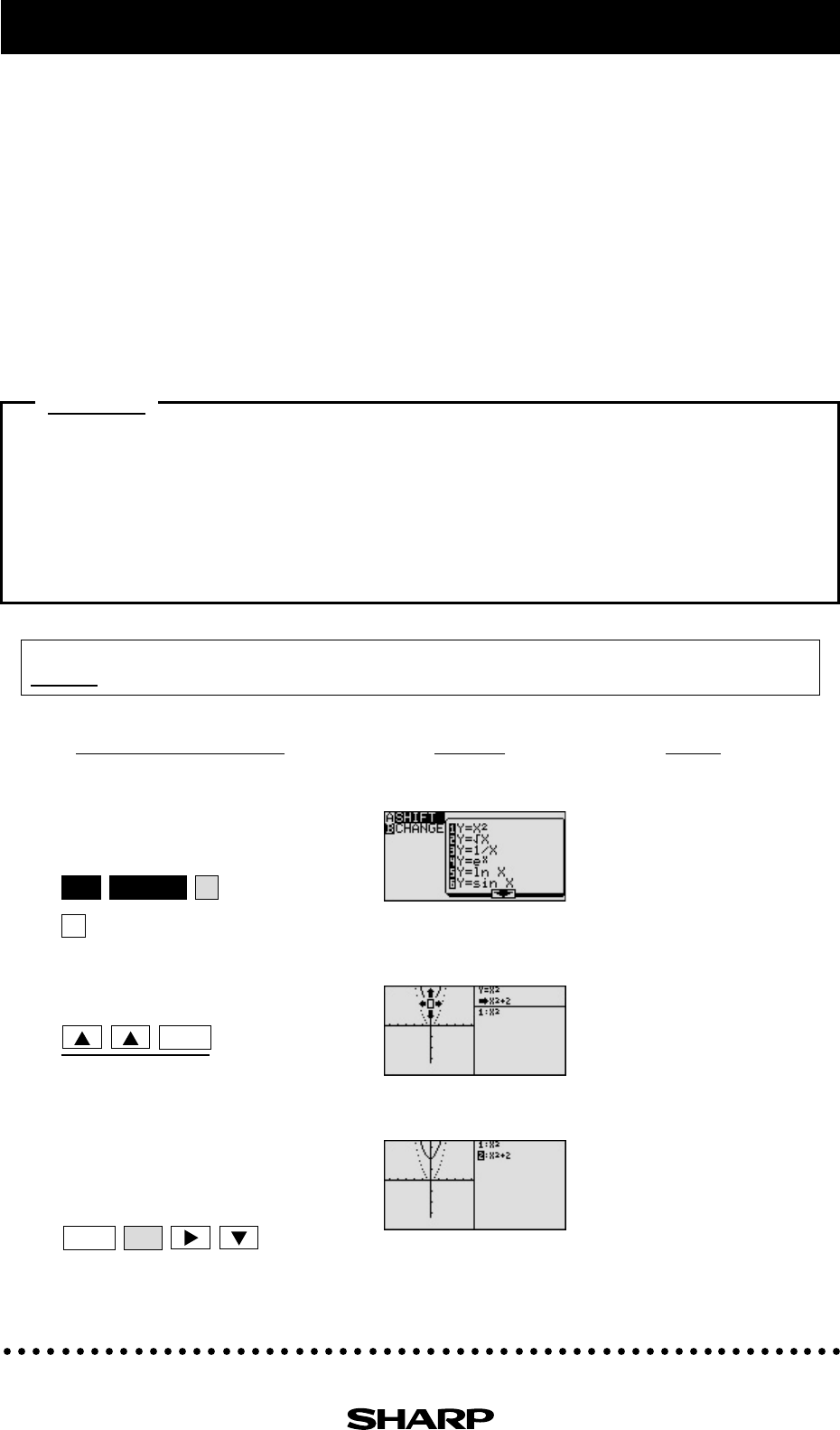
1-1 Access Shift feature and select the
equation y = x
2
.
*
*
1-2
Move the graph y = x
2
upward by 2.
*
Save the new graph and observe the
changes in the graph and the
equation.
1-3
Notice that upward movement
of the basic y =
x
2
graph by 2
units in the direction of the y-
axis means addition of 2 to the
y-intercept. This demonstrates
that upward movement of the graph by k units means
adding a k (>0) in the standard form y = a (x - h)
2
+ k.
1
2nd F
SHIFT/CHANGE
A
ENTER
ENTER
ALPHA
Before
Starting


















