EL-9650/9600c/9450/9400 Graphing Calculator
8-4
There may be differences in the results of calculations and graph plotting depending on the setting.
Return all settings to the default value and delete all data.
Set viewing window to “-5< x <50,” and “-10< y <10” using Rapid Window feature to solve Q1.
*
*
*
NotesStep & Key Operation
(When using EL-9650/9600c)
*Use either pen touch or cursor to operate.
Display
(When using EL-9650/9600c)
Solving Absolute Value Inequalities
To solve an inequality means to find all values that make the inequality true. Absolute value
inequalities are of the form |
f (x)
|<
k,
|
f (x)
|
≤
k,
|
f (x)
|>
k,
or
|
f (x)
|
≥
k.
The graphical
solution to an absolute value inequality is found using the same methods as for normal
inequalities. The first method involves rewriting the inequality so that the right-hand side of
the inequality is 0 and the left-hand side is a function of x. The second method involves
graphing each side of the inequality as an individual function.
Solve absolute value inequalities in two methods.
Example
1-2
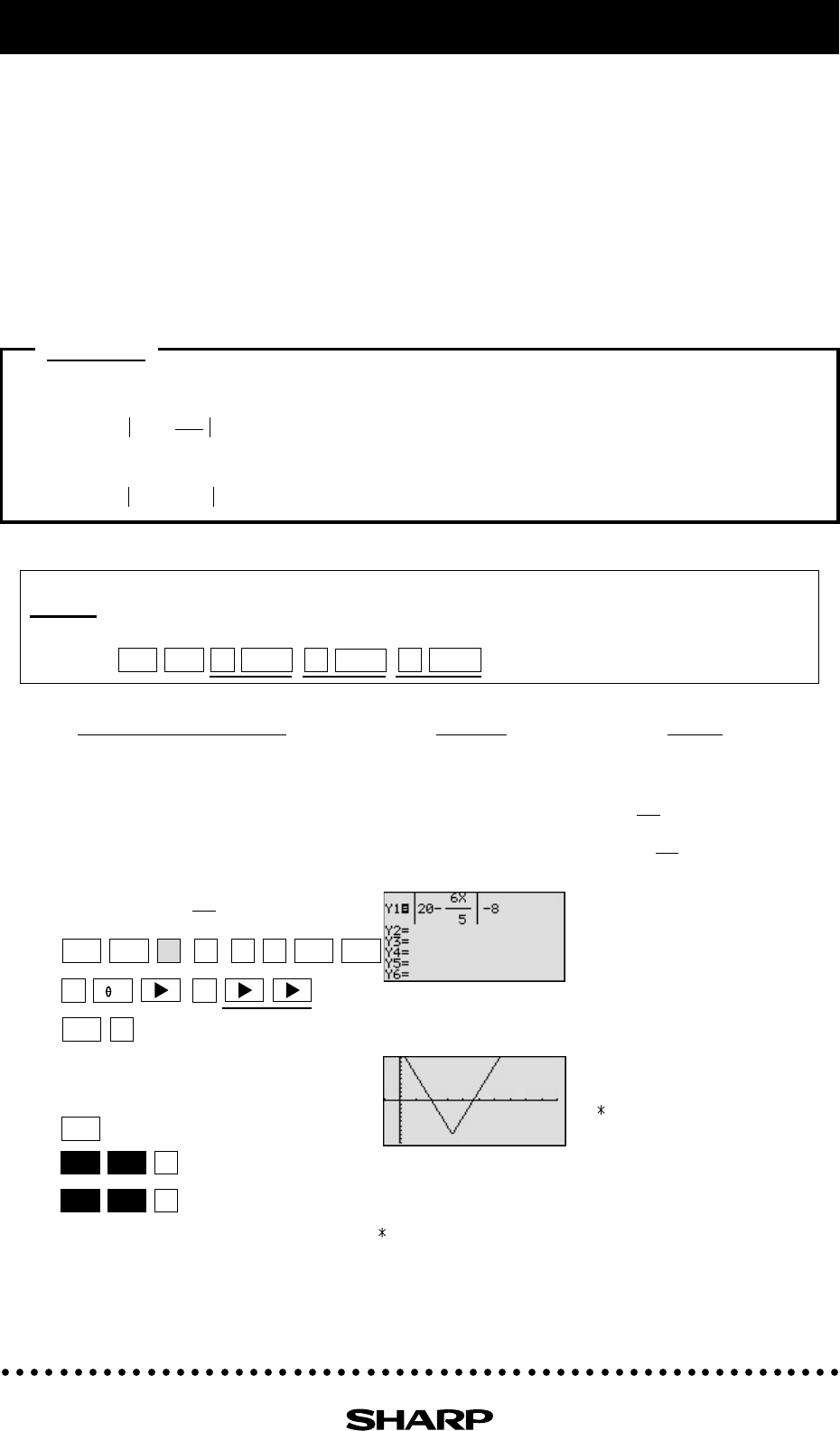
Enter y = |20 - | - 8 for Y1.
*
*
*
*
1-1
Rewrite the equation.
|20 - |< 8
➞|20 - | - 8 < 0.
1-3
View the graph, and find the
x-intercepts.
*
➞ x = 10, y = 0
*
➞ x = 23.33333334
y = 0.00000006 ( Note)
The intersections with the x-
axis are (10, 0) and (23.3, 0)
(
Note: The value of y in the
x-intercepts may not appear
exactly as 0 as shown in the
example, due to an error
caused by approximate calcu-
lation.)
1-4
Solve the inequality.
Since the graph is below the
x-axis for x in between the
two x-intercepts, the solution
is 10 < x < 23.3.
6x
5
6x
5
1. Solve 20 - < 8 by rewriting the inequality so that the right-hand side of
the inequality is zero.
2. Solve 3.5x + 4 > 10 by shading the solution region.
6x
5
WINDOW
EZ333
ENTER ENTER ENTER
GRAPH
2nd F CALC
2nd F CALC
B520
6
8
5
5
5
Y=
MATH
—
—
a
/b
6x
5
X/
/T/n
Before
Starting
02.10.28, 1:15 PMPage 2


















