AN42 APPLICATION NOTE
12
Table 8. R
sense
for various load currents
Discrete Sense Resistor
Discrete iron alloy resistors come in a variety of tolerances
and power ratings, and are ideal for precision implementa-
tions. Either an MnCu alloy wire resistor or an CuNi alloy
wire resistor is ideal for a low cost implementation.
Embedded Sense Resistor (PC Trace Resistor)
Embedded PC trace resistors have the advantage of almost
zero cost implementation. However, the value of the PC
trace resistors have large variations. Embedded resistors
have 3 major error sources: the sheet resistivity of the inner
layer, the mismatch due to L/W, and the temperature varia-
tion of the resistor. When laying out embedded sense resis-
tors, consider all error sources described as follows:
• Sheet resistivity.
For 1 ounce copper, the thickness variation is typically
between 1.15 mil and 1.35 mil. Therefore, the error due to
sheet resistivity is (1.35 – 1.15)/1.25 = 16%.
• Mismatch due to L/W.
The error in L/W is dictated by the geometry and the
power dissipation capability of the sense resistor. The
sense resistor must be able to handle the load current and,
therefore, requires a minimum width, calculated as
follows:
where W is the minimum width required for proper power
dissipation (mils), and I
L
is the load current in Amps.
For a load current of 15A, the minimum width required is
300mils, which reflects a 1% L/W error.
• Thermal Considerations.
The I
2
R power losses cause the surface temperature of the
resistor to increase along with its resistance value. In
addition, ambient temperature variations add the change
in resistor value:
where R
20
is the resistance at 20°C, α
20
= 0.00393/ °C,T
is the operating temperature, andR is the desired value.
For temperature T = 50°C, the %R change = 12%.
Table 9 is a summary of tolerances for the Embedded PC
Trace Resistor.
Table 9. Summary PC Trace Resistor Tolerance
Design rules for using an embedded resistor
The basic equation for laying an embedded resistor is:
where ρ is the Resistivity (W-mil), L is the Length (mils), W
is the Width (mils), and t is the Thickness (mils).
For 1oz copper, t = 1.35 mils, ρ = 717.86 µΩ-mil,
1 L/1 W = 1 Square ( ■ ).
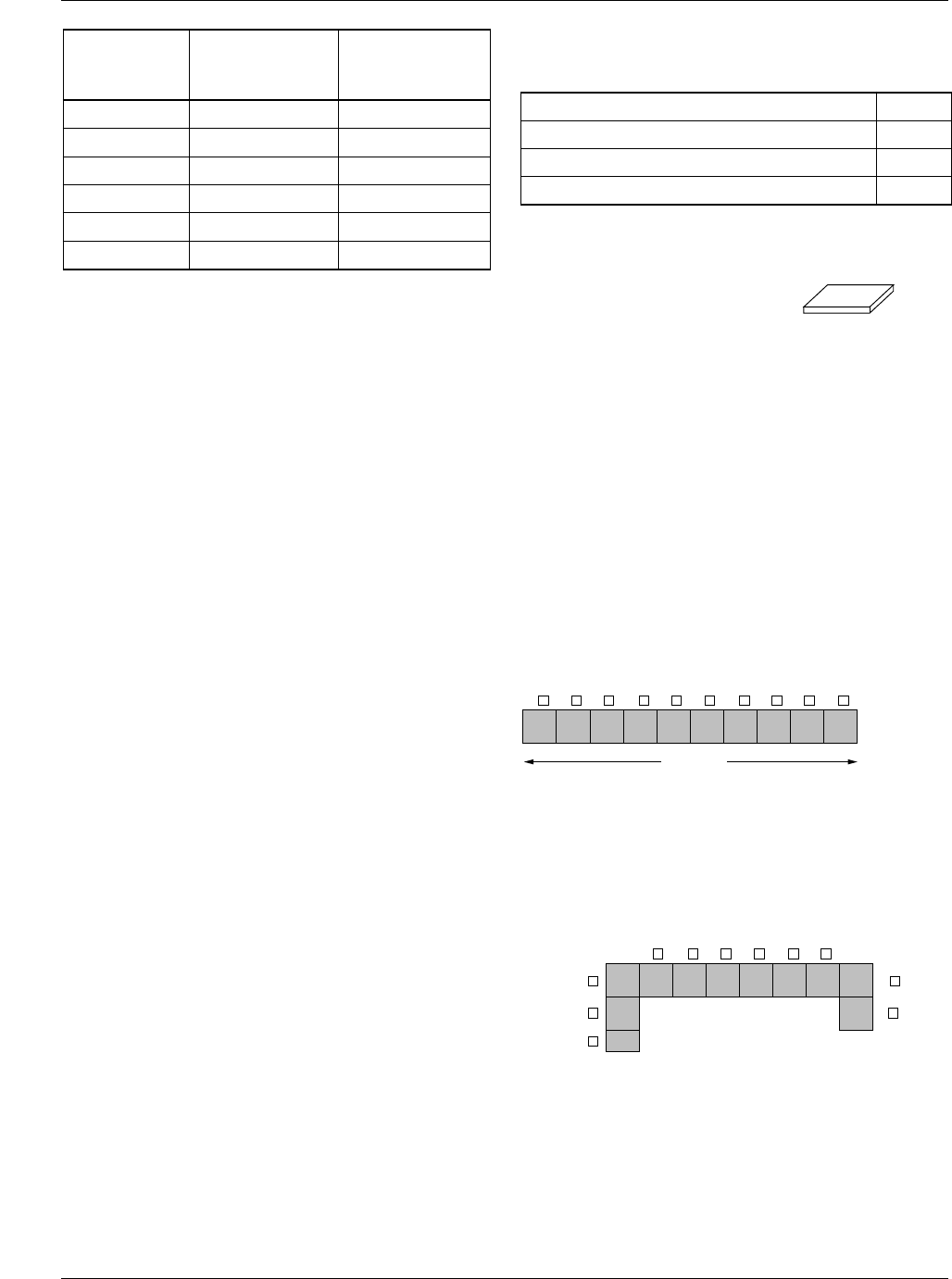
For example, you can layout a 5.30mΩ embedded sense
resistor. From Equations above,
L/W = 10 ■.
Therefore, to model 5.30mΩ enbedded resistor, you need
W = 200 mils, and L = 2000 mils. See Figure 10.
Figure 10. 5.30mΩ Sense Resistor (10 ■)
You can also implement the sense resistor in the following
manner. Each corner square is counted as 0.6 square since
the current flowing through the corner square does not flow
uniformly, concentrated towards the inside edge. This is
shown in Figure 11.
Figure 11. 5.30mΩ Sense Resistor (10 ■)
A Resign Example Combining an Embedded Resistor
with a Discrete Resistor
For low cost implementation, the embedded PC trace resistor
is the most desirable alternative, but, as discussed earlier, the
wide tolerance (±29%) presents a challenge. In addition,
changing CPU requirements may force the maximum load
I
Load,max
(A)
R
SENSE
PC Trace
Resistor (mΩ)
R
SENSE
Discrete
Resistor (mΩ)
10.0 6.5 8.6
11.2 5.8 7.8
12.4 5.3 7.1
13.9 4.8 6.4
14.0 4.7 6.3
14.5 4.6 6.1
W
I
L
0.05
----------=
R R
20
1 α
20
T 20–( )]+[=
Tolerance due to sheet resistivity variation 16%
Tolerance due to L/W error 1%
Tolerance due to temperature variation 12%
Total Tolerance for PC Trace Resistor 29%
R ρ
L
W t×
-------------
×=
W
I
L
0.05
----------
10
0.05
---------- 200mil= = =
L
R W× t×
ρ
-----------------------
0.00530 200× 1.35×
717.86
--------------------------------------------------- 2000m
i
= = =
1 1 1 1 1 1 1 1 1 1
W = 200 mils
L = 2000
.6 .6
.8
1 1 1 1 1 1
1 1
W
L
t