E-59
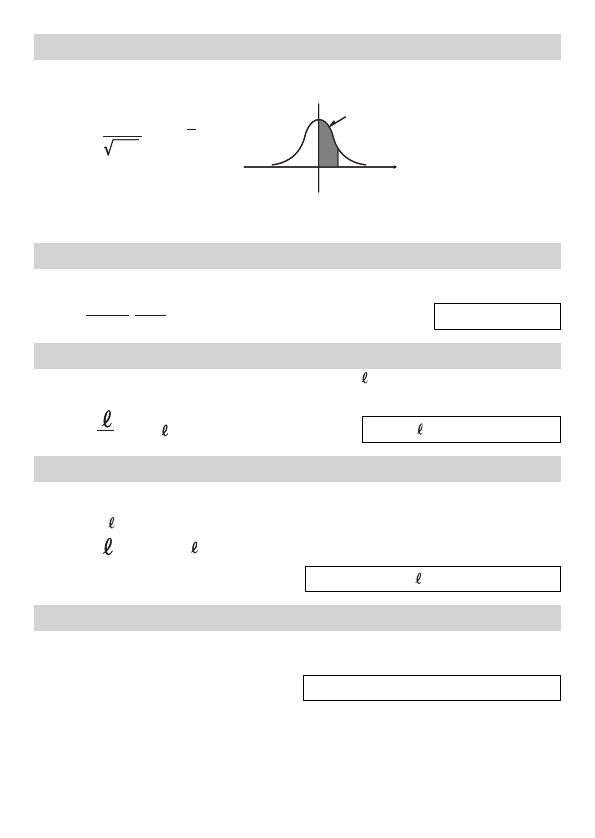
No. 05 Normal Probability Function Q(
x
)
Uses Hastings’ estimate formula to determine the probability of a standard normal
distribution Q(
x
) illustrated below when the standardized variate (
x
) is known.
Important!
Since this is an estimate formula, proper precision may not be obtainable.
No. 06 Coulomb’s Law
Determines the force (
F
) between two charges of quantities
Q
and
q
, over a separation of
r
.
(
Ƥ
0
: permittivity)
Q(x) = edt
(0 x < 1 × 10
50
)
2π
1
|
x
|
∫
2
2
t
−
0
Q x
x
Q(x) = edt
(0 x < 1 × 10
50
)
2π
1
|
x
|
∫
2
2
t
−
0
Q x
x
F =
Qq
(r > 0)
4πε
0
1
r
2
F =
Qq
(r > 0)
4πε
0
1
r
2
Units:
Q
,
q
: C,
r
: m
No. 07 Resistance of a Conductor
Determines resistance
R
of a conductor when its length ( ) and cross sectional area (
S
),
and the resistance of its component material (
ρ
) are known.
R =
ρ
(S, ,
ρ
> 0)
S
R =
ρ
(S, ,
ρ
> 0)
S
Units: : m,
S
: m
2
,
ρ
:
Ω
·m,
R
:
Ω
No. 08 Magnetic Force
Determines the motive force (
F
) in a conductor with electric current (
I
) fl owing through it
and placed in a magnetic fi eld of uniform magnetic force density (
B
), when the length of the
conductor is
and the angle formed by the conductor and magnetic fi eld is
Ƨ
.
Units:
B
: T,
I
: A, : m,
Ƨ
: ° (degrees),
F
: N
No. 09 Change in Terminal Voltage of R in an RC Series Circuit
Determines the terminal voltage (
V
R
) of terminal
R
at time
t
in an RC series circuit when
voltage
V
is applied to a circuit with a resistance of
R
and capacitance of
C
.
F = IB
( > 0, 0˚
| |
90˚)
sin
θ
θ
F = IB
( > 0, 0˚
| |
90˚)
sin
θ
θ
VR = V•e
−t/CR
(C, R, t > 0)
VR = V•e
−t/CR
(C, R, t > 0)
Units:
R
:
Ω
,
C
: F,
t
: seconds,
V
and
V
R
: V


















