95
Chapter 8: Application Examples
P (X
1
, Y
1
)
S (X
3
, Y
3
)
Q (X
2
, Y
2
)
O (X, Y)
X
1
–X
Y
1
–Y
R
R
R
(X
1
2
+Y
1
2
-X
2
2
-Y
2
2
)(Y
2
–Y
3
) – (X
2
2
+Y
2
2
-X
3
2
-Y
3
2
)(Y
1
–Y
2
)
2{(X
1
–X
2
)(Y
2
–Y
3
) – (X
2
–X
3
)(Y
1
–Y
2
)}
X = ------ 1
(X
1
2
+Y
1
2
-X
2
2
-Y
2
2
)(X
2
–X
3
) – (X
2
2
+Y
2
2
-X
3
2
-Y
3
2
)(X
1
–X
2
)
2{(Y
1
–Y
2
)(X
2
–X
3
) – (Y
2
–Y
3
)(X
1
–X
2
)}
Y = ------ 2
R =
(X – X
1
)
2
+ (Y – Y
1
)
2
------ 3
GM – HK
2 (IM – JK)
X =
GJ – HI
2 (KJ – MI)
Y =
* Calculate intermediate
values.
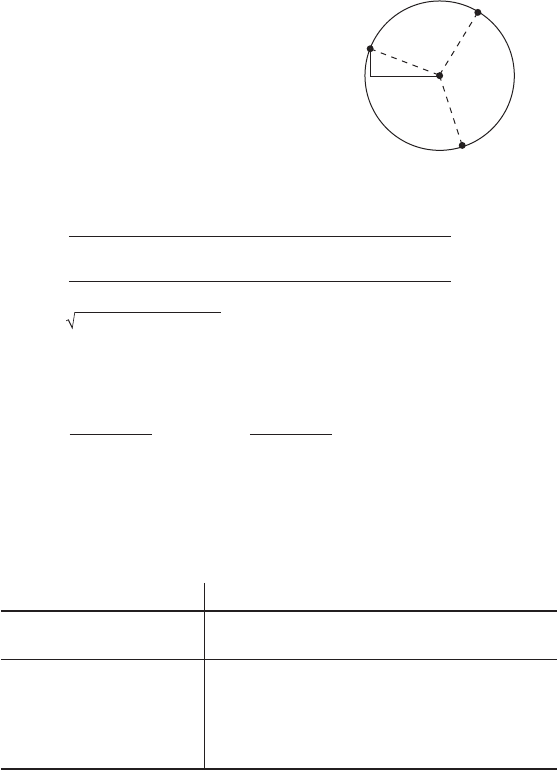
A circle that passes through 3 points
When three different points, P (X1, Y1), Q (X2, Y2), S (X3, Y3) are given,
obtain the center coordinates O (X, Y) and the radius R of the circle that
passes through these points.
To satisfy the above conditions, the
distances between P, Q, S and O
should be equal. as they are the
radius of the same circle. Therefore,
PO = QO = SO = R
Using the Pythagorean theorem,
PO
2
=
(
X1 – X
)
2
+
(
Y1 – Y
)
2
= R
2
QO
2
=
(
X2 – X
)
2
+
(
Y2 – Y
)
2
= R
2
SO
2
=
(
X3 – X
)
2
+
(
Y3 – Y
)
2
= R
2
then
To enhance both readability and writability of the program, intermediate
variables G, H, I, J, K and M are used.
The above equations reduce to
1.
Press b 2 1 0 to open a window for creating a NEW program.
2. Type CIRCLE for the title then press e.
•A NEW program called ‘CIRCLE’ will be created.
3. Enter the program as follows.
Program code Key operations
Print”ENTER COORDS i 1 @ a ENTER s COORDS
; e
G=X≥Œ+Y≥Œ-X√Œ-Y√Œ ; G ; = @ v X1 e
e A + @ v d Y1 e
e A - @ v d d X2
e e A - @ v d
d d Y2 e e A e


















