single three-phase reading.
Some digital meters calculate the individual phase power values one phase at a time. This means the
meter samples the voltage and current on one phase and calculates a power value. Then it samples the
second phase and calculates the power for the second phase. Finally, it samples the third phase and
calculates that phase power. After sampling all three phases, the meter combines the three readings to
create the equivalent three-phase power value. Using mathematical averaging techniques, this method
can derive a quite accurate measurement of three-phase power.
More advanced meters actually sample all three phases of voltage and current simultaneously and
calculate the individual phase and three-phase power values. The advantage of simultaneous sampling
is the reduction of error introduced due to the difference in time when the samples were taken.
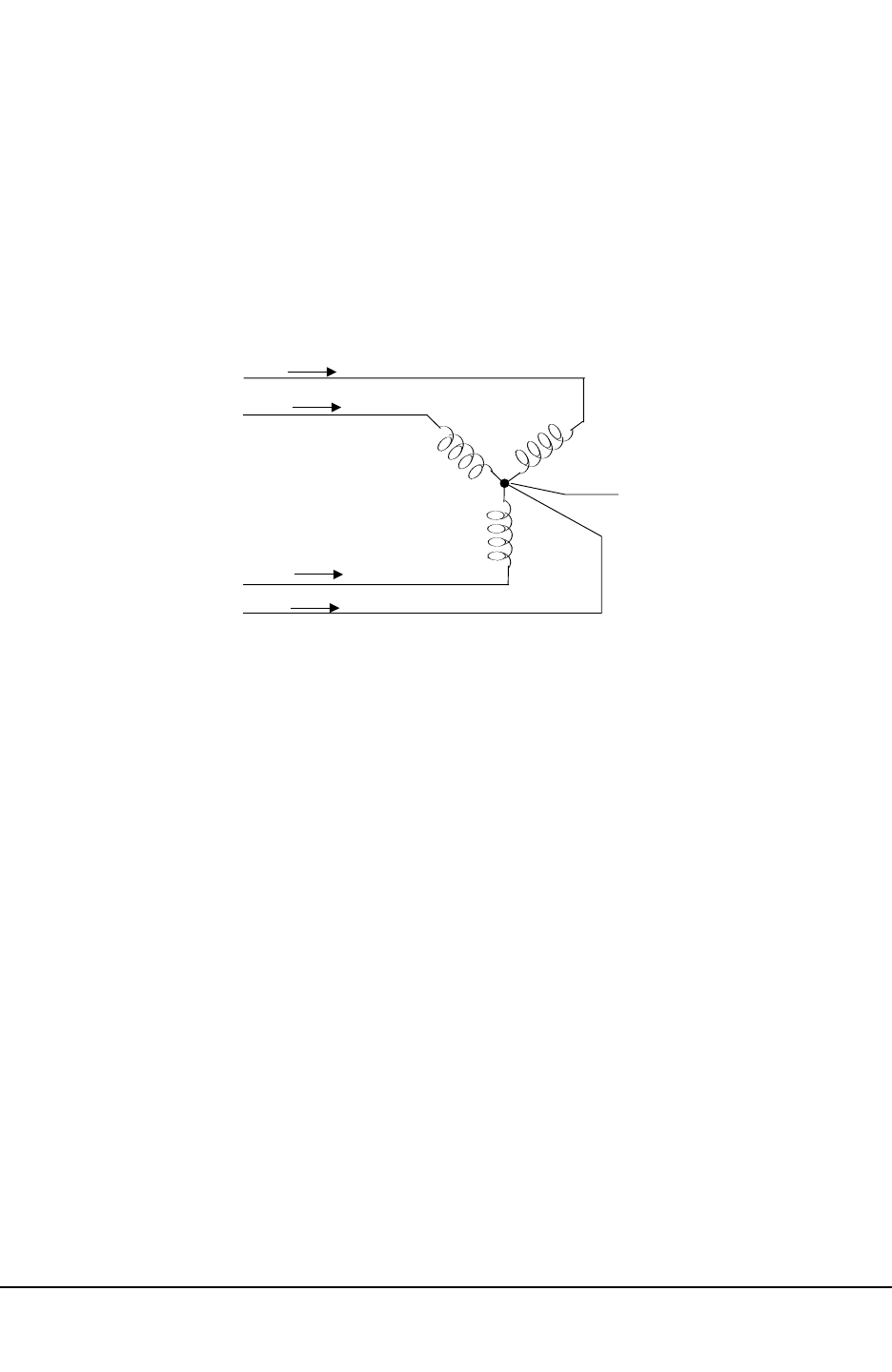
Blondell's Theorem is a derivation that results from Kirchhoff's Law. Kirchhoff's Law states that the
sum of the currents into a node is zero. Another way of stating the same thing is that the current into a
node (connection point) must equal the current out of the node. The law can be applied to measuring
three-phase loads. Figure 1.6 shows a typical connection of a three-phase load applied to a three-
phase, four-wire service. Krichhoff's Laws hold that the sum of currents A, B, C and N must equal zero
or that the sum of currents into Node "n" must equal zero.
If we measure the currents in wires A, B and C, we then know the current in wire N by Kirchhoff's
Law and it is not necessary to measure it. This fact leads us to the conclusion of Blondell's Theorem
that we only need to measure the power in three of the four wires if they are connected by a common
node. In the circuit of Figure 1.6 we must measure the power flow in three wires. This will require
three voltage coils and three current coils (a three element meter). Similar figures and conclusions
could be reached for other circuit configurations involving delta-connected loads.
Electro Industries/GaugeTech
Doc # E107706 V1.25 1-5
Phase A
Phase B
Phase C
Figure 1.6: Three-Phase Wye Load illustrating Kirchhoff’s Law
and Blondell’s Theorem
Node “n”
A
B
N
C


















