Page 11-5
where f
(n)
(x) represents the n-th derivative of f(x) with respect to x, f
(0)
(x) = f(x).
If the value x
0
= 0, the series is referred to as a Maclaurin’s series.
Functions TAYLR, TAYLR0, and SERIES
Functions TAYLR, TAYLR0, and SERIES are used to generate Taylor
polynomials, as well as Taylor series with residuals. These functions are
available in the CALC/LIMITS&SERIES menu described earlier in this Chapter.
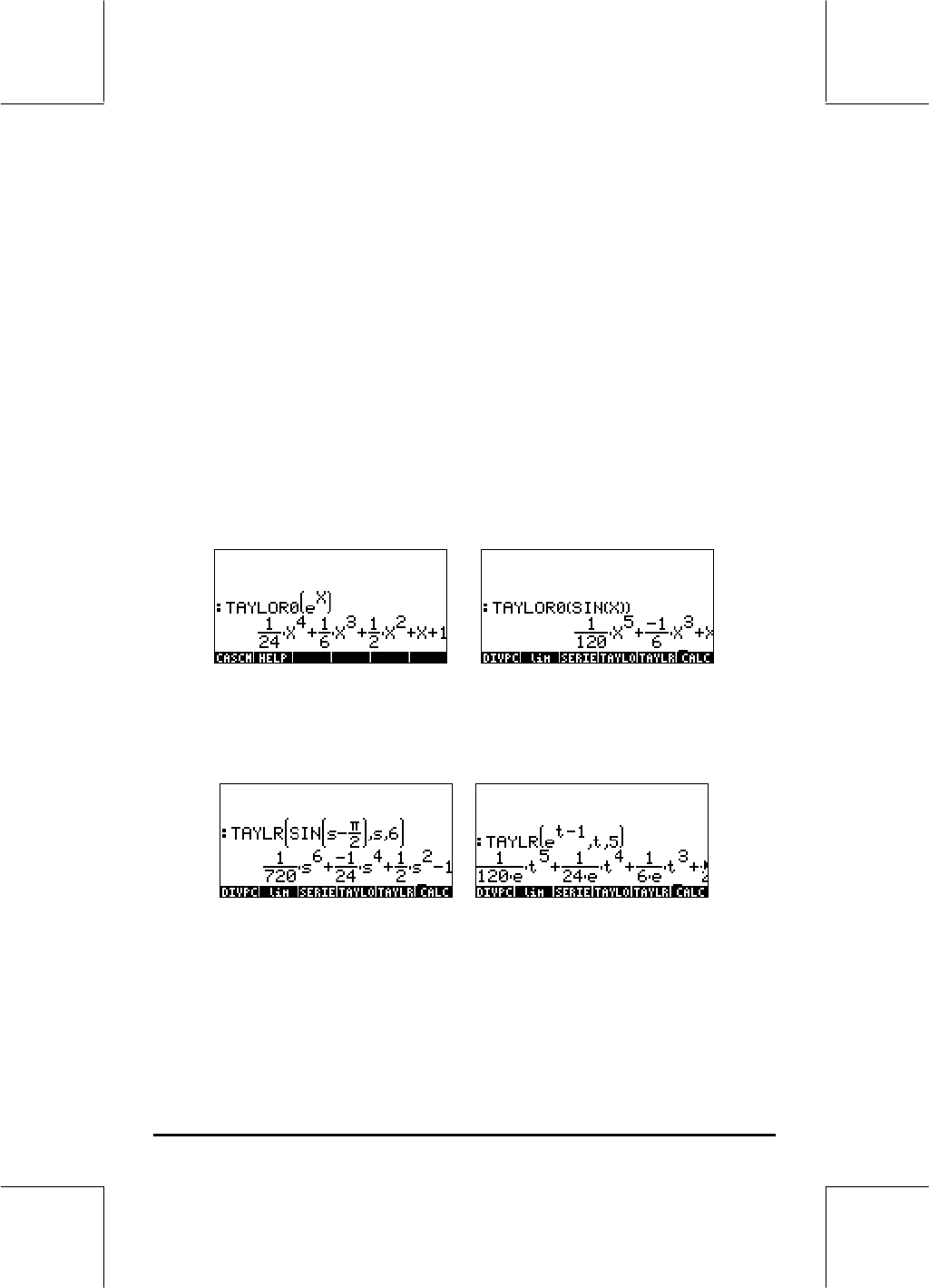
Function TAYLOR0 performs a Maclaurin series expansion, i.e., about X = 0,
of an expression in the default independent variable, VX (typically ‘X’). The
expansion uses a 4-th order relative power, i.e., the difference between the
highest and lowest power in the expansion is 4. For example,
Function TAYLR produces a Taylor series expansion of a function of any
variable x about a point x = a for the order k specified by the user. Thus, the
function has the format TAYLR(f(x-a),x,k). For example,
Function SERIES produces a Taylor polynomial using as arguments the
function f(x) to be expanded, a variable name alone (for Maclaurin’s series)
or an expression of the form ‘variable = value’ indicating the point of
expansion of a Taylor series, and the order of the series to be produced.
Function SERIES returns two output items a list with four items, and an


















