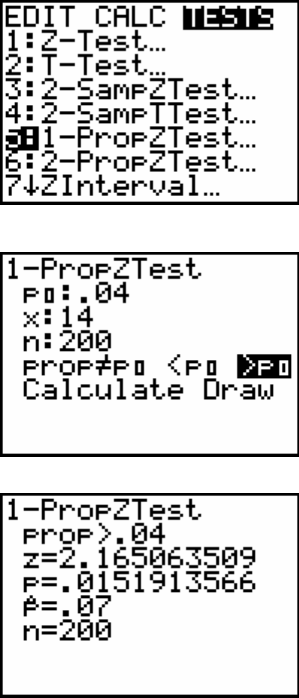
defective chips. Test at the 5% significance level whether or not the machine needs an
adjustment.
Our hypotheses are H
0
: p = 4% and H
1
: p > 4%. We will use 1-PropZTest, with p
0
= 0.04,
x = 14, n = 200, and p
1
> p
0
for our alternative hypothesis.
Press the STAT key.
Press the ► key twice to highlight TESTS.
Press the number 5 key.
Type in .04 for p
0.
Type in 14 for x.
Type in 200 for n.
Move the cursor over >P
0
and press the ENTER key.
Move the cursor over Calculate and press the ENTER key.
The 1-PropZTest output shows the
alternative hypothesis: prop > .04
test statistic: Z=2.165063509
p-value: P=.0151913566
sample proportion: ê=.07
sample size: n=200
The p-value is 0.015, which is less than 5%; we reject H
0
and conclude that the machine does
need adjustment.
Example: Quality Control
Direct Mailing Company sells computers and computer parts by mail. The company claims that
at least 90% of all orders are mailed within 72 hours after they are received. The quality control
department at the company often takes samples to check if this claim is valid. A recently taken
sample of 150 orders showed that 129 of them were mailed within 72 hours. Do you think the
company’s claim is true? Use a 2.5% significance level. Our hypotheses are H
0
: p = .90 and H
1:
p < .90. We will use the 1-PropZTest, with p
0
= 0.90, x = 129, n = 150, and p
1
< p
0
for our
alternative hypothesis.
58
