Filter
Top Products
Exercises
Use the following sample data for the exercises in this chapter.
Height (in) 67 71 62 66 74 64 72 74
Weight (lbs) 195 220 100 168 225 130 180 190
1. Compute a regression model for this data and also find the coefficient of determination and
the linear correlation coefficient.
2. Use the model to estimate the weight of someone who is 5’8”, i.e., 68 inches tall.
3. Sketch a scatter diagram with the regression line.
4. Test at a 5% significance level whether or not B = 0 for the population based on this sample
data.
Solutions
1. The linear regression model is y’ = -358.82 + 7.78X.
The coefficient of determination is r
2
= .703.
The linear correlation coefficient is r = .839.
2. The estimated weight is Y
1
(68) = 170.17.
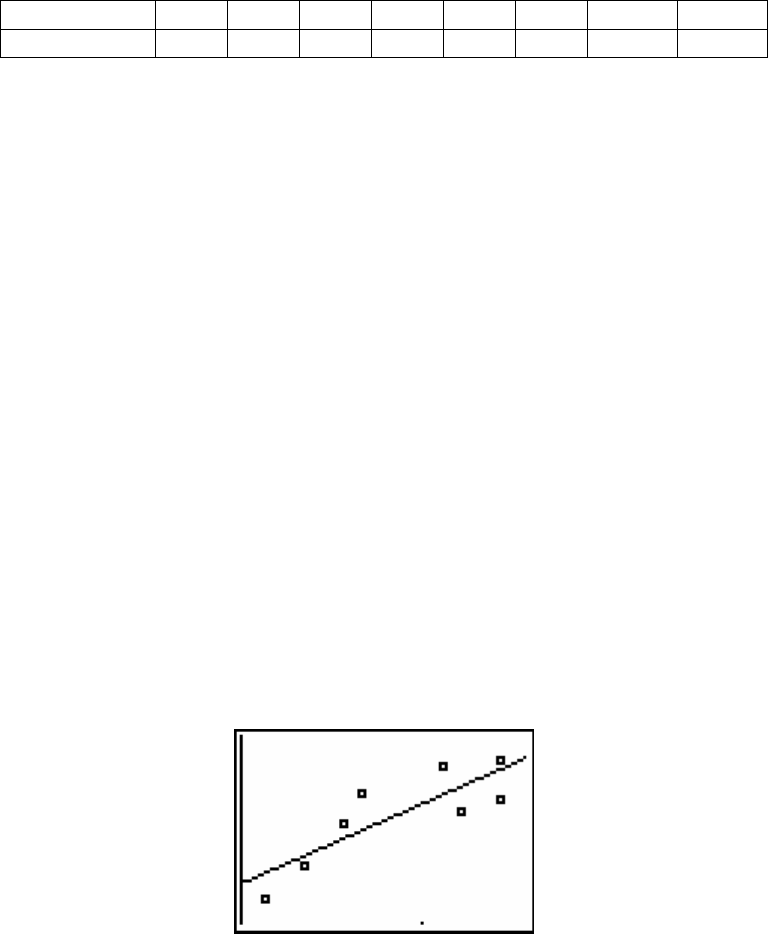
3. The scatterplot with regression line.
4. Using LinRegTTest the p-value is .005 which is less than our significance level of 5%
we reject the null hypothesis and conclude that B is significantly greater than zero.
83