Chapter 2 Robustness Analysis
MATRIXx Xmath Robust Control Module 2-2 ni.com
system, including how the uncertain transfer functions are connected to the
system and the magnitude bound functions l
i
(w).
To do this, extract the uncertain transfer functions and collect them into a
k-input, k-output transfer matrix Δ, where:
(2-2)
The resulting closed-loop system can be viewed as a feedback connection
of the nominal closed-loop system with transfer matrix H(jω) and the
uncertain transfer matrix Δ(jω). You describe your nominal closed-loop
system as a linear system with
input and output .
Note The signals r and q are not really inputs and outputs of the nominal system; r and q
show how the uncertain transfer functions connect to your nominal system. The signals r
and q each have k components.
You will partition H into the four submatrices,
so that H
zw
is the nominal transfer matrix from w to z, H
zr
is the nominal
transfer matrix from r to z, H
qw
is the nominal transfer matrix from w to q,
and H
qr
is the nominal transfer matrix from r to q.
The magnitude bound functions l
i
(jω) from Equation 2-1 are described
with the PDM
delb:
Thus, a complete description of your system requires the system
SysH
to represent H
jw
and the response delb to represent the bounds.
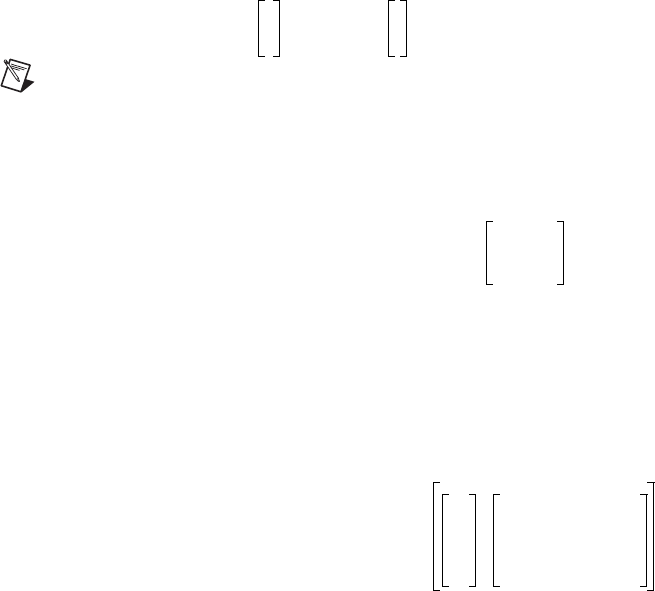
Δ jω() diagonal δ
1
jω(),...,δ
k
jω()()=
w
r
z
q
H
H
zw
H
zr
H
qw
H
qr
=
DELB
ω
1
:
ω
m
l
1
ω
1
()…l
k
ω
1
()
::
l
1
ω
m
()…l
k
ω
m
()
,
=


















