Chapter 4 Controller Synthesis
MATRIXx Xmath Robust Control Module 4-6 ni.com
Selecting these weights has much the same effect here. Specifically, let H
zv
be the closed-loop transfer matrix (with u = K
γ
) from inputs:
to outputs:
Thus,
Suppose that the controller u = K
y
approximates Equation 4-2. Thus,
In many cases, this means that the maximum singular value of the
frequency response matrix (W
out
H
zv
W
in
)( jω) is constant over all
frequencies. That is,
An interpretation is that the weighting filters W
in
and W
out
determine the
shape of the closed-loop frequency response H
zw
( jω), and γ
opt
determines
the peak value. This observation helps motivate the selection of the weights
so as to shape the closed-loop frequency response matrix H
zw
( jω).
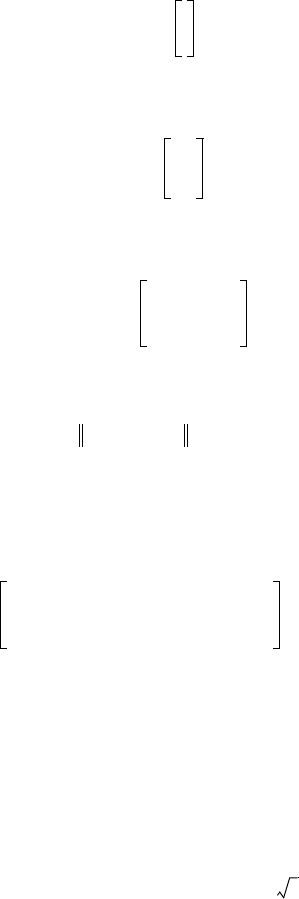
Observe, however, that the elements of the frequency response matrix,
(W
out
H
zv
W
in
)( jω), need not be constant. Instead, the maximum singular
value of at least one of the four subblocks is within 3 dB of γ
opt
. For all ω,
v
d
n
=
z
y
reg
u
=
H
zv
H
y
reg
d
H
y
reg
n
H
ud
H
un
=
W
out
H
zv
W
in
∞
γ
opt
≈
σ
max
W
reg
H
y
reg
d
W
dist
W
reg
H
y
reg
n
W
noise
W
act
H
ud
W
dist
W
act
H
jn
W
noise
jw()
⎝⎠
⎜⎟
⎜⎟
⎛⎞
γ
opt
≈
M ω() σ
max
W
out
H
zv
W
in
()jω()[]2M ω()≤≤


















