Statistics Programs 16-11
Example 2:
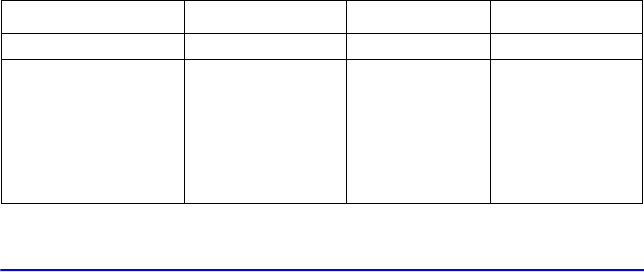
Repeat example 1 (using the same data) for logarithmic, exponential, and power
curve fits. The table below gives you the starting execution label and the results (the
correlation and regression coefficients and the x– and y– estimates) for each type of
curve. You will need to reenter the data values each time you run the program for a
different curve fit.
Normal and Inverse–Normal Distributions
Normal distribution is frequently used to model the behavior of random variation
about a mean. This model assumes that the sample distribution is symmetric about
the mean, M, with a standard deviation, S, and approximates the shape of the bell–
shaped curve shown below. Given a value x, this program calculates the probability
that a random selection from the sample data will have a higher value. This is
known as the upper tail area, Q(x). This program also provides the inverse: given a
value Q(x), the program calculates the corresponding value x.
Calculates regression coefficient B.
Calculates regression coefficient M.
Prompts for hypothetical x–value.
Stores 37 in X and calculates .
Stores 101 in Y and calculates .
Logarithmic Exponential Power
To start:
LEP
R 0.9965 0.9945 0.9959
B –139.0088 51.1312 8.9730
M 65.84460.01770.6640
Y ( when X=37)
98.7508 98.5870 98.6845
X ( when Y=101)
38.2857 38.3628 38.3151
y
ˆ
x
ˆ
y
ˆ
x
ˆ


















