E-8 More about Integration
This is the correct answer, but it took a very long time. To understand why, compare
the graph of the function between x = 0 and x = 10
3
, which looks about the same
as that shown in the previous example, with the graph of the function between x = 0
and x = 10:
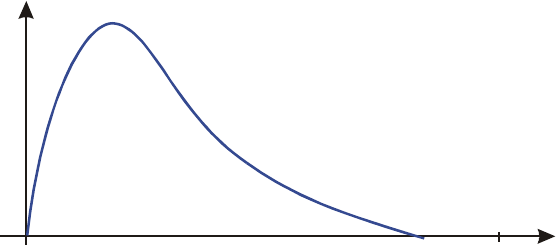
You can see that this function is "interesting" only at small values of x. At greater
values of x, the function is not interesting, since it decreases smoothly and gradually
in a predictable manner.
The algorithm samples the function with higher densities of sample points until the
disparity between successive approximations becomes sufficiently small. For a
narrow interval in an area where the function is interesting, it takes less time to
reach this critical density.
To achieve the same density of sample points, the total number of sample points
required over the larger interval is much greater than the number required over the
smaller interval. Consequently, several more iterations are required over the larger
interval to achieve an approximation with the same accuracy, and therefore
calculating the integral requires considerably more time.
X
∫
Integral. (The calculation takes a
minute or two.)
Uncertainty of approximation.
x
f (x)
0 10


















