Filter
Top Products
Page 12-2
Multiple integrals
A physical interpretation of the double integral of a function f(x,y) over a
region R on the x-y plane is the volume of the solid body contained under the
surface f(x,y) above the region R. The region R can be described as R =
{a<x<b, f(x)<y<g(x)} or as R = {c<y<d, r(y)<x<s(y)}. Thus, the double integral
can be written as
∫∫∫∫∫∫
==
d
c
ys
yr
b
a
xg
xf
R
dydxyxdydxyxdAyx
)(
)(
)(
)(
),(),(),(
φφφ
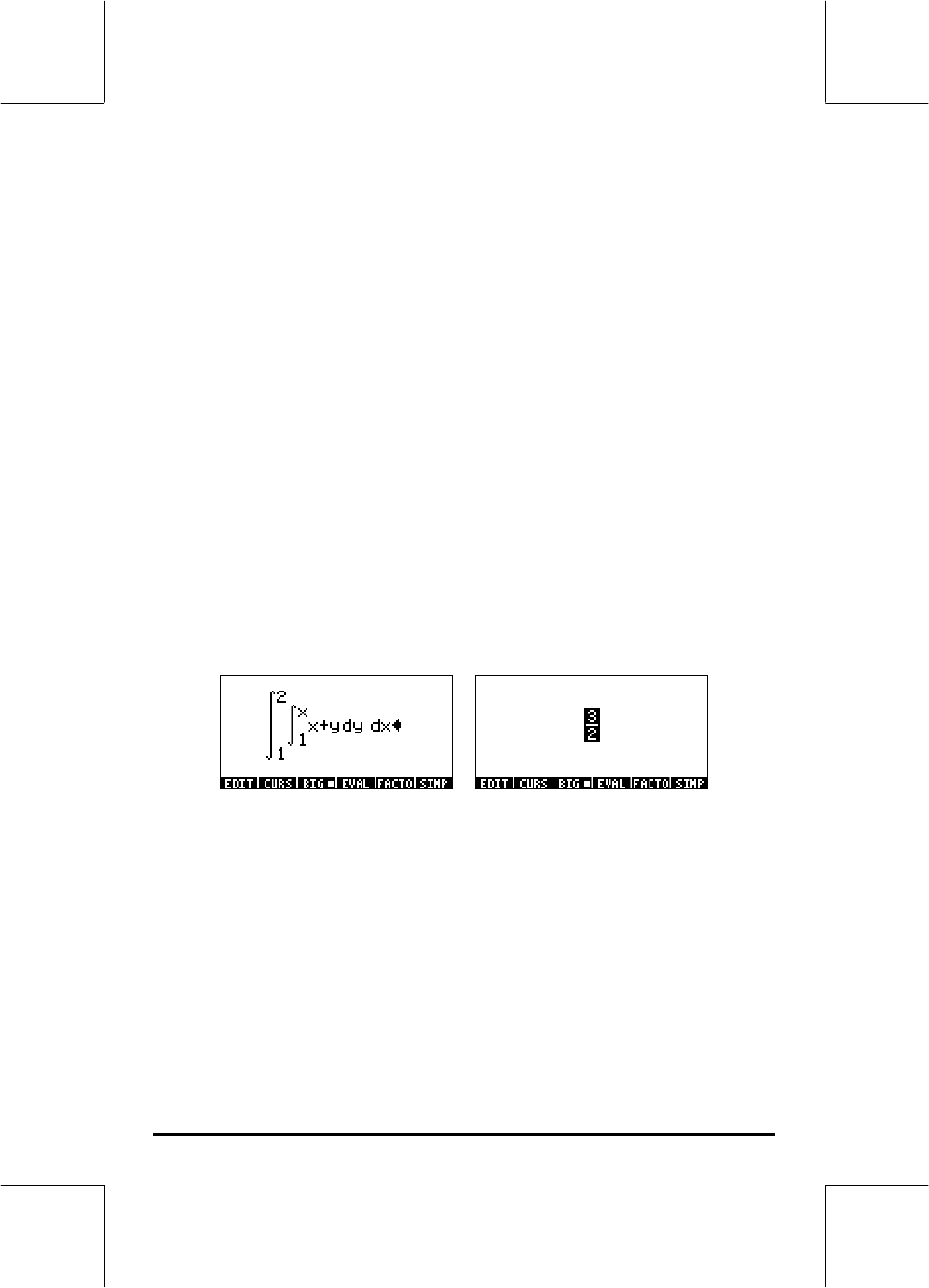
Calculating a double integral in the calculator is straightforward. A double
integral can be built in the Equation Writer (see example in Chapter 2), as
shown below. This double integral is calculated directly in the Equation
Writer by selecting the entire expression and using function
@EVAL
. The result is
3/2.
Reference
For additional details of multi-variate calculus operations and their
applications see Chapter 14 in the calculator’s user guide.