Page 13-1
Chapter 13
Vector Analysis Applications
This chapter describes the use of functions HESS, DIV, and CURL, for
calculating operations of vector analysis.
The del operator
The following operator, referred to as the ‘del’ or ‘nabla’ operator, is a vector-
based operator that can be applied to a scalar or vector function:
[] [] [] []
z
k
y
j
x
i
∂
∂
⋅+
∂
∂
⋅+
∂
∂
⋅=∇
When applied to a scalar function we can obtain the gradient of the function,
and when applied to a vector function we can obtain the divergence and the
curl of that function. A combination of gradient and divergence produces the
Laplacian of a scalar function.
Gradient
The gradient of a scalar function φ(x,y,z) is a vector function defined by
φ
φ
∇=grad . Function HESS can be used to obtain the gradient of a
function.. The function takes as input a function of n independent variables
φ(x
1
, x
2
, …,x
n
), and a vector of the functions [‘x
1
’ ‘x
2
’…’x
n
’]. The function
returns the Hessian matrix
of the function, H = [h
ij
] = [∂φ/∂x
i
∂x
j
], the gradient
of the function with respect to the n-variables, grad f = [ ∂φ/∂x
1
∂φ/∂x
2
…
∂φ
/
∂
x
n
], and the list of variables [‘x
1
’, ‘x
2
’,…,’x
n
’]. This function is easier to
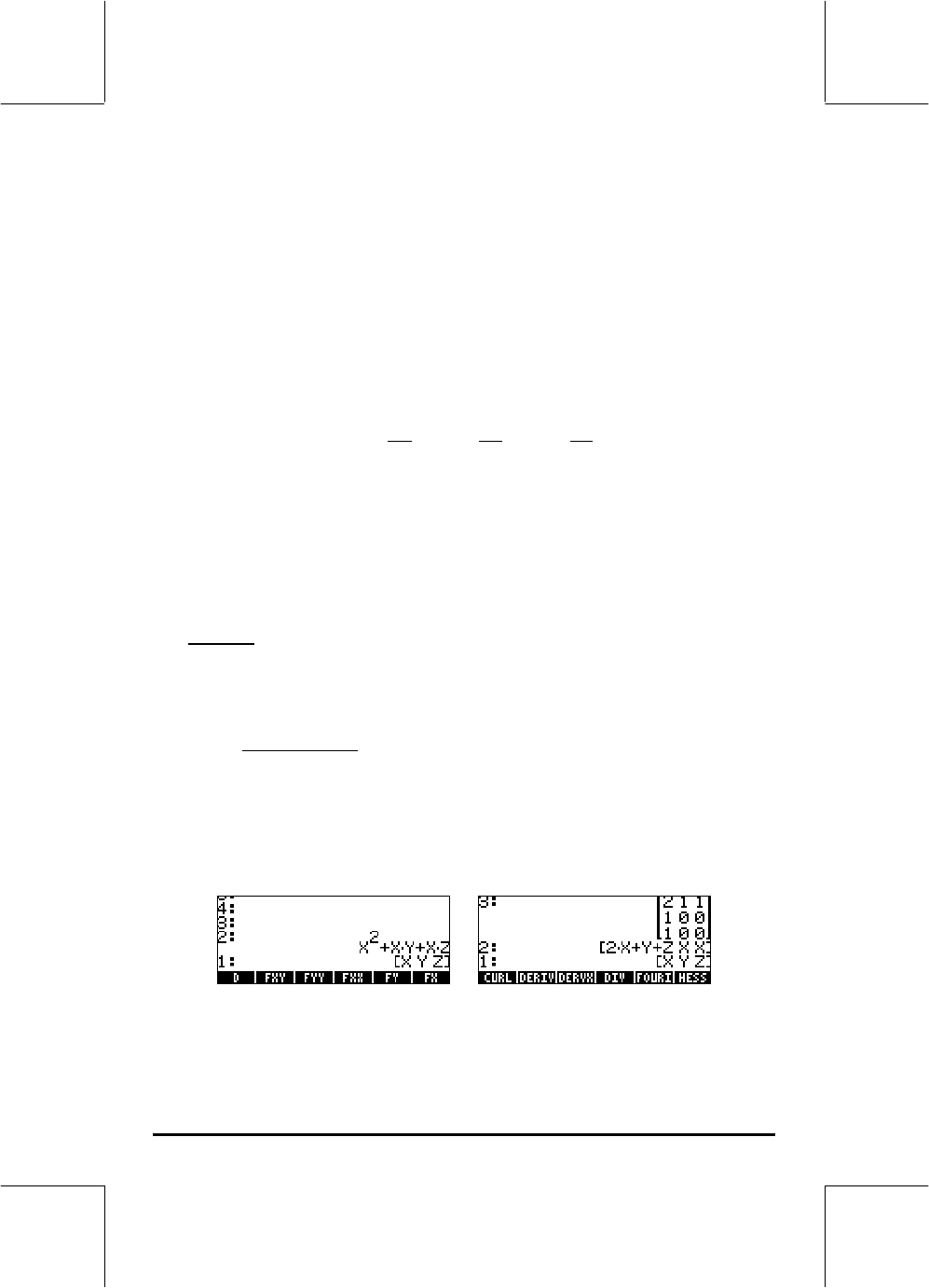
visualize in the RPN mode. Consider as an example the function φ(X,Y,Z) =
X
2
+ XY + XZ, we’ll apply function HESS to this scalar field in the following
example:
Thus, the gradient is [2X+Y+Z, X, X].


















