Filter
Top Products
Chapter 2 Robustness Analysis
MATRIXx Xmath Robust Control Module 2-12 ni.com
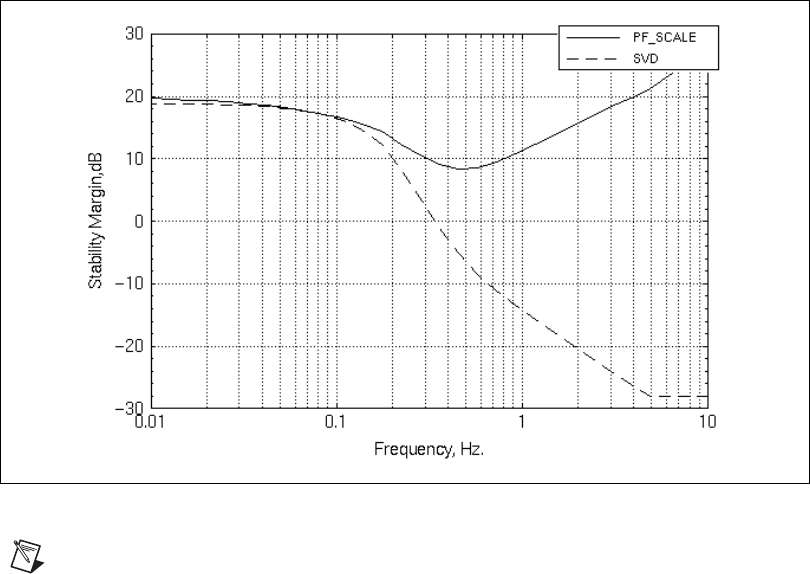
You can compare this margin to that of the example in the Creating a
Nominal System section; the following inputs produce Figure 2-7.
plot ([marg,margSVD],{xlog}
legend=["PF_SCALE","SVD"],
ylab="Stability Margin,dB",
xlab="Frequency, Hz."})
Figure 2-7. pfscale( ) versus svd Stability Margins
Note
The singular value approach gives results that are too conservative, suggesting that
the uncertainties can destabilize the system. Conversely, you know from the scaled singular
value calculations that the system is robustly stable.
Approximation with Scaled Singular Values
In [Saf82] and [Doy82], the inequality
(2-5)
is noted. This optimization problem can be shown to be
unimodal—for D>0, an assumption that can be made without loss
min σ
max
DMD
1–
()μM()≥
D diagonal