Setting up
26
- ENGLISH
Getting Started
Screen size and throw distance
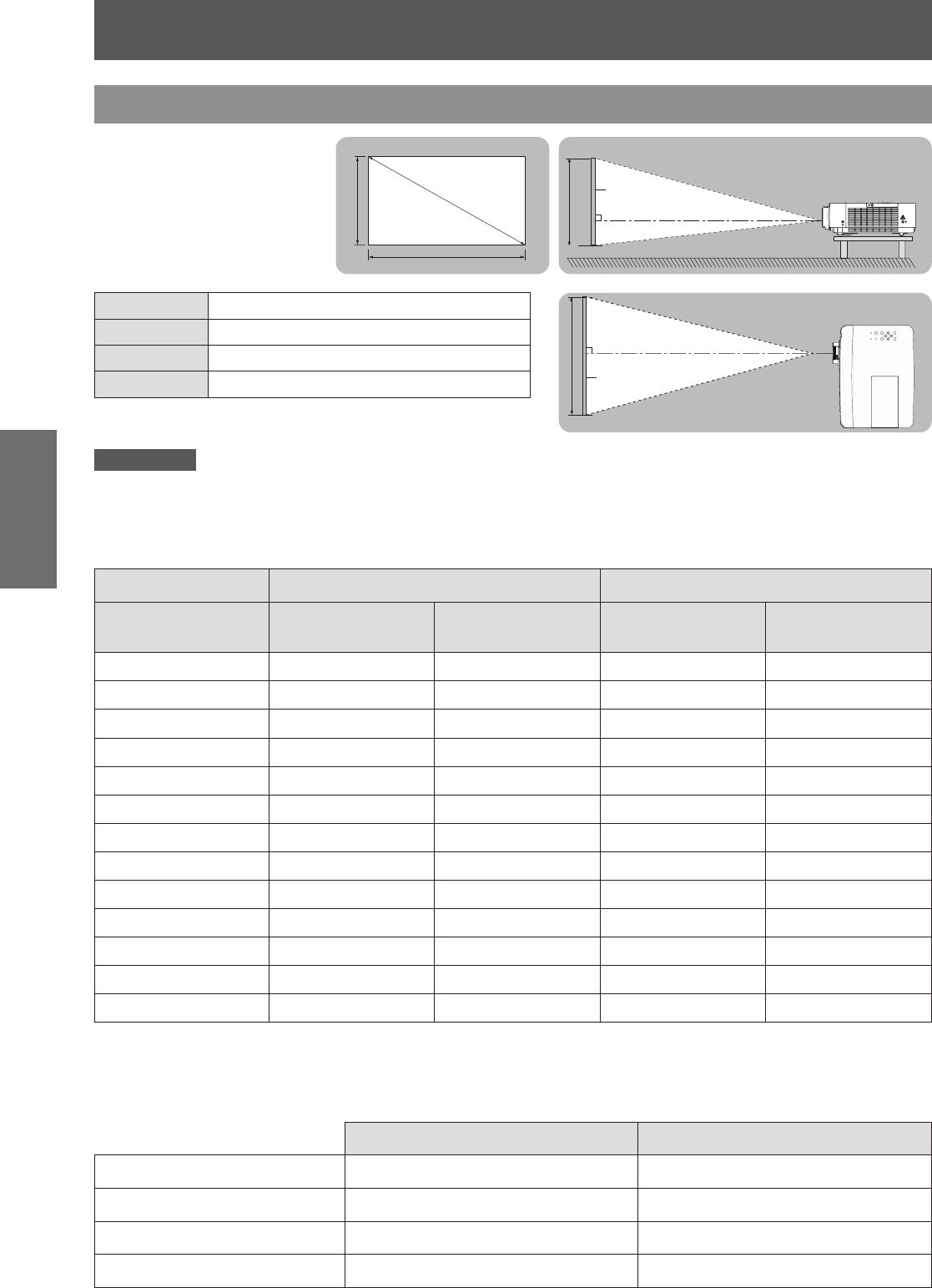
Place the projector referring
to the diagram on the right
and the gures of throwing
distance. You can adjust the
display size
L (LW/LT)
Screen
L (LW/LT)
SW
Screen
SH
SW
SD
Projected image
SH
L (LW/LT) *
1
Projection distance (m)
SH Height of the projection area (m)
SW Width of the projection area (m)
SD Diagonal length of the projection area (m)
LW : Minimum distance *1 :
LT : Maximum distance
Attention
Before installing, please read “Precautions for Use” (
z
Æ
pages 14 to 18).
J
Projection distance for PT-VX400NTU
(All measurements below are approximate and may differ slightly from the actual measurements.)
Projection size For 4:3 aspect ratio For 16:9 aspect ratio
Screen diagonal (SD)
Minimum distance
(LW)
Maximum distance
(LT)
Minimum distance
(LW)
Maximum distance
(LT)
0.76 m(30") 0.7 m(2.26') 1.1 m(3.74') 0.8 m(2.49') 1.2 m(4.07')
1.02 m(40") 0.9 m(3.05') 1.5 m(5.02') 1.0 m(3.35') 1.7 m(5.48')
1.27 m(50") 1.2 m(3.87') 1.9 m(6.30') 1.3 m(4.23') 2.1 m(6.89')
1.52 m(60") 1.4 m(4.66') 2.3 m(7.58') 1.6 m(5.09') 2.5 m(8.27')
1.78 m(70") 1.7 m(5.45') 2.7 m(8.86') 1.8 m(5.94') 3.0 m(9.68')
2.03 m(80") 1.9 m(6.23') 3.1 m(10.14') 2.1 m(6.82') 3.4 m(11.06')
2.29 m(90") 2.2 m(7.05') 3.5 m(11.42') 2.3 m(7.68') 3.8 m(12.47')
2.54 m(100") 2.4 m(7.84') 3.9 m(12.73') 2.6 m(8.53') 4.2 m(13.88')
3.05 m(120") 2.9 m(9.42') 4.7 m(15.29') 3.1 m(10.27') 5.1 m(16.67')
3.81 m(150") 3.6 m(11.81') 5.8 m(19.13') 3.9 m(12.86') 6.4 m(20.83')
5.08 m(200") 4.8 m(15.78') 7.8 m(25.52') 5.2 m(17.19') -
6.35 m(250") 6.0m(19.75') - 6.6 m(21.52') -
7.62 m(300") 7.2 m(23.72') - 7.9 m(25.85') -
Any other projection distance can be obtained according to the screen dimensions (m) using the following calculations.
The distance is shown in units of meters. (The calculated distance may contain a certain error.)
If the screen dimensions are written as “SD",
For 4:3 aspect ratio For 16:9 aspect ratio
Screen height (SH) = SD(m) × 0.6 = SD(m) × 0.490
Screen width (SW) = SD(m) × 0.8 = SD(m) × 0.872
Minimum distance (LW) = 0.9531 × SD(m) - 0.0338 = 1.0384 × SD(m) - 0.0337
Maximum distance (LT) = 1.5384 × SD(m) - 0.0327 = 1.6756 × SD(m) - 0.0319


















