Filter
Top Products
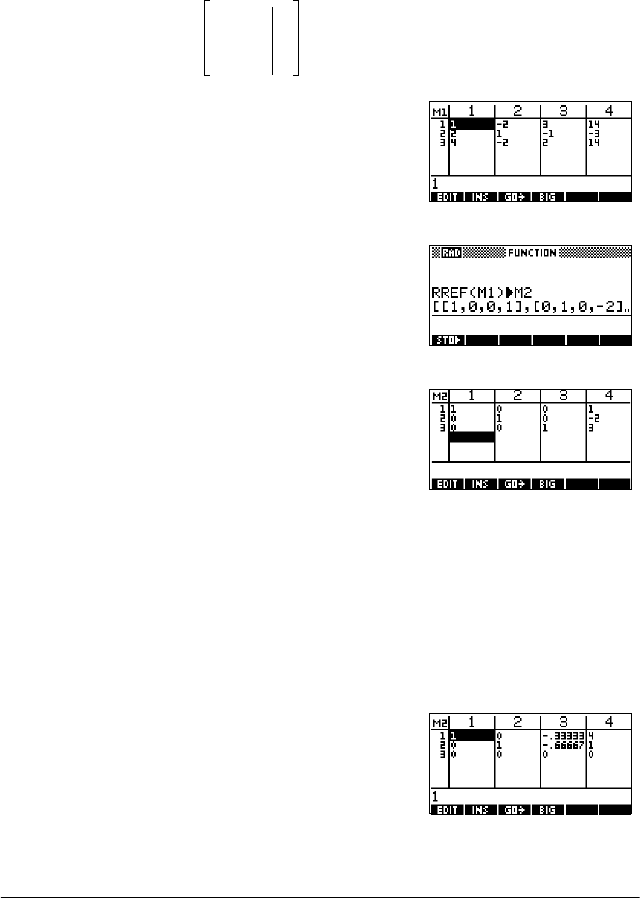
13-14 Matrices
Reduced-Row
Echelon Form
The following set of equations
can be written as the augmented matrix
which can then stored as a
real matrix in any
matrix variable. M1 is used
in this example.
You can use the RREF
function to change this to
reduced row echelon form,
storing it in any matrix
variable. M2 is used in this
example.
The reduced row echelon
matrix gives the solution to
the linear equation in the
fourth column.
An advantage of using the
RREF function is that it will also work with inconsistent
matrices resulting from systems of equations which have
no solution or infinite solutions.
For example, the following set of equations has an infinite
number of solutions:
The final row of zeros in the
reduced-row echelon form
of the augmented matrix
indicates an inconsistency.
x 2y–3z+14
2xyz–+3
4x
–
2y–2z+14
=
=
=
12–314
21 1–3–
42–214
34×
xyz–+5
2xy–7
x 2y– z+2
=
=
=