139
Miscellaneous
Learning Curve for Manufacturing Costs
Many production process costs vary with output according to the "learning
curve" equation. The production team becomes more proficient in
manufacturing a given item as more and more of them are fabricated and
costs may be expected to decrease by a predictable amount. The learning
factor, r, characterizes the learning curve. For instance, if r=.80 the curve
is called an 80% learning curve.
It is readily apparent that the learning, or experience curve, has many
uses in setting production standards, forecasting costs, setting prices, etc.
Note, however, that the learning factor may change, especially after large
numbers have been produced.
It the cost of the first unit of a run, C
1
, and the learning curve factor, r, are
known, the following procedure can be used to calculate the cost of the
nth item:
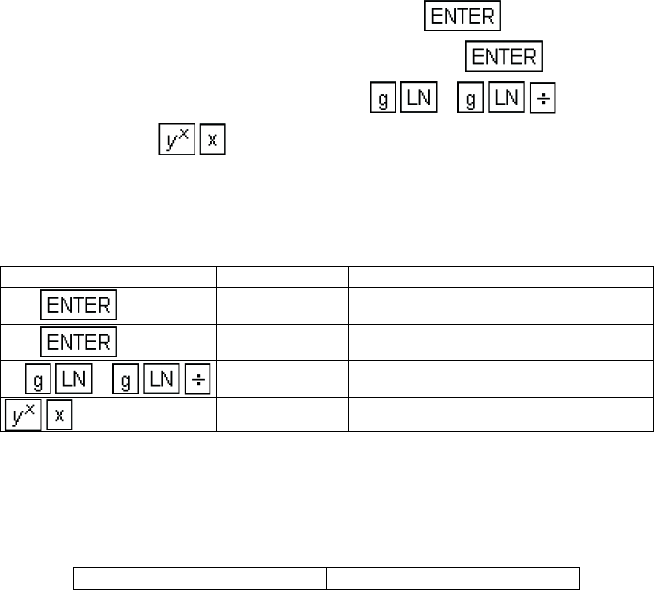
1. Key in the cost of the first item, C
1
and press .
2. Key in the number of units produced, n, and press .
3. Key in the learning factor, r, and press 2 .
4. Then press to calculate the cost of the nth unit, C
n
.
Example 1: An electronic manufacturer begins a pilot run on a new
instrument. From past experience he expects the process to have a
learning factor, r, or 0.90. If the first unit costs $875 to produce, what is the
expected cost of the 100th unit?
If the cost of the first unit, C
1
, and the nth unit, C
n
, are known the learning
factor may be calculated. In addition, it is possible to calculate C
ij
, the
average cost of the ith thru jth unit. These calculations may be rapidly
done with the following HP-12C program:
Keystrokes Display
875
875.00
100
100.00
.9 2
-0.15
434.51 Cost of the 100th unit.
KEYSTROKES DISPLAY


















