143
Queuing and Waiting Theory
Waiting lines, or queues, cause problems in many marketing situations.
Customer goodwill, business efficiency, labor and space considerations
are only some of the problems which may be minimized by proper
application of queuing theory.
Although queuing theory can be complex and complicated subject,
handheld calculators can be used to arrive at helpful decisions.
One common situation that we can analyze involves the case of several
identical stations serving customers, where the customers arrive randomly
in unlimited numbers. Suppose there are n (1 or more) identical stations
serving the customers. λ is the arrival rate (Poisson input) and µ is the
service rate (exponential service). We will assume that all customers are
served on a firstcome, first-served basis and wait in a single line (queue)
then are directed to whichever station is available. We also will assume
that no customers are lost from the queue. This situation, for instance,
would be closely approximated by customers at some banking operations.
The formulas for calculating some of the necessary probabilities are too
complex for simple keystroke solution. However, tables listing these
probabilities are available and can be used to aid in quick solutions. Using
the assumptions outlined above and a suitable table giving mean waiting
time as a multiple of mean service (see page 512 of the Reference) the
following keystroke solutions may be obtained:
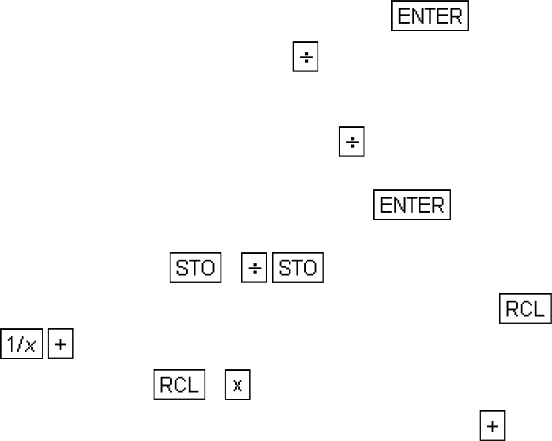
1. Key in the arrival rate of customers, λ, and press .
2. Key in the service rate, µ, and press to calculate ρ, the intensity
factor. (Note ρ must be less than n for valid results, otherwise the queue
will lengthen without limit).
3. Key in n, the number of servers and press to calculate ρ/n.
4. For a given n and ρ/n find the mean waiting time as a multiple of mean
service time from the table. Key it in and press .
5. Calculate the average waiting time in the queue by keying in the service
rate, µ, and pressing 1 2.
6. Calculate the average waiting time in the system by pressing 1
.
7. Key in λ and press 2 to calculate the average queue length.
8. Key in ρ, then intensity factor (from step 2 above) and press to
calculate the average number of customer in the system.
Reference:


















