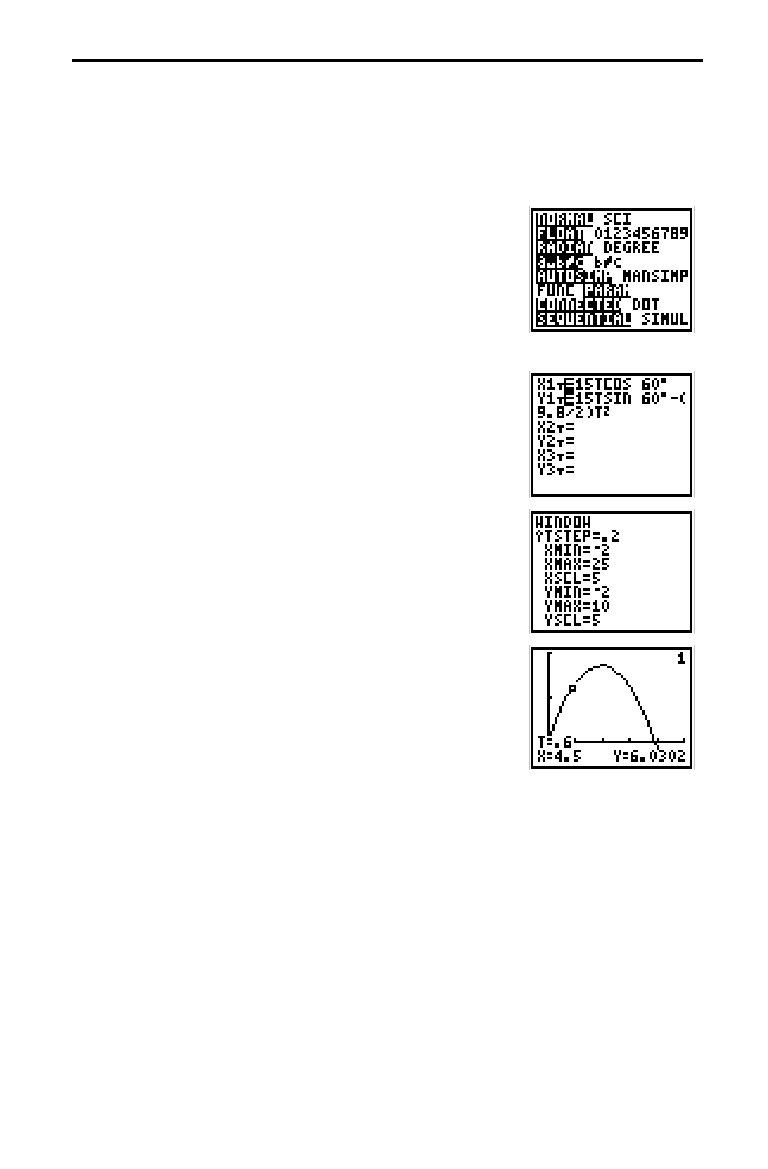
5-2 Parametric Graphing
Getting Started is a fast-paced introduction. Read the chapter for details.
Graph the parametric equation that describes the path of a ball kicked at an
angle of 60
¡
with an initial velocity of 15 meters per second. (Ignore air
resistance.) What is the maximum height? When does the ball strike the ground?
1. Press
3
, and then press
8
8
8
8
8
9
¸
to
select
PARAM
mode.
For initial velocity v
0
and angle
q
, the horizontal
component of the ball as a function of time is
X(t) = t v
0
cos
q
. The vertical component is
Y(t) = t v
0
sin
q
-
(g
à
2) t
2
. The gravity constant g is
9.8 m
à
sec
2
.
2. Press
(
. Press
15
@
X
60
2
E
1
(to select
¡
)
¸
to define the
X
portion of the parametric
equation in terms of
T
.
3. Press
15
@
W
60
2
E
1
(to select
¡
)
|
c
9.8
e
2
d
@
a
¸
to define the
Y
portion.
4. Press
)
. Enter the Window variables
appropriate for this problem.
TMIN=0 XMIN=
ë
2 YMIN=
ë
2
TMAX=3 XMAX=25 YMAX=10
TSTEP=.2 XSCL=5 YSCL=5
5. Press
+
to graph the position of the ball as a
function of time.
Tracing begins at
TMIN
. As you press
9~
to trace the
curve, the cursor follows the path of the ball over
time. The values for
X
(distance),
Y
(height), and
T
(time) are displayed at the bottom of the screen.
The maximum height is approximately 8.6 meters. The
ball strikes the ground in approximately 2.6 seconds.
Getting Started: Path of a Ball


















