Page 11-5
Infinite series
A function f(x) can be expanded into an infinite series around a point x=x
0
by using a Taylor’s series, namely,
,
where f
(n)
(x) represents the n-th derivative of f(x) with respect to x, f
(0)
(x) =
f(x).
If the value x
0
= 0, the series is referred to as a Maclaurin’s series.
Functions TAYLR, TAYLR0, and SERIES
Functions TAYLR, TAYLR0, and SERIES are used to generate Taylor
polynomials, as well as Taylor series with residuals. These functions are
available in the CALC/LIMITS&SERIES menu described earlier in this
Chapter.
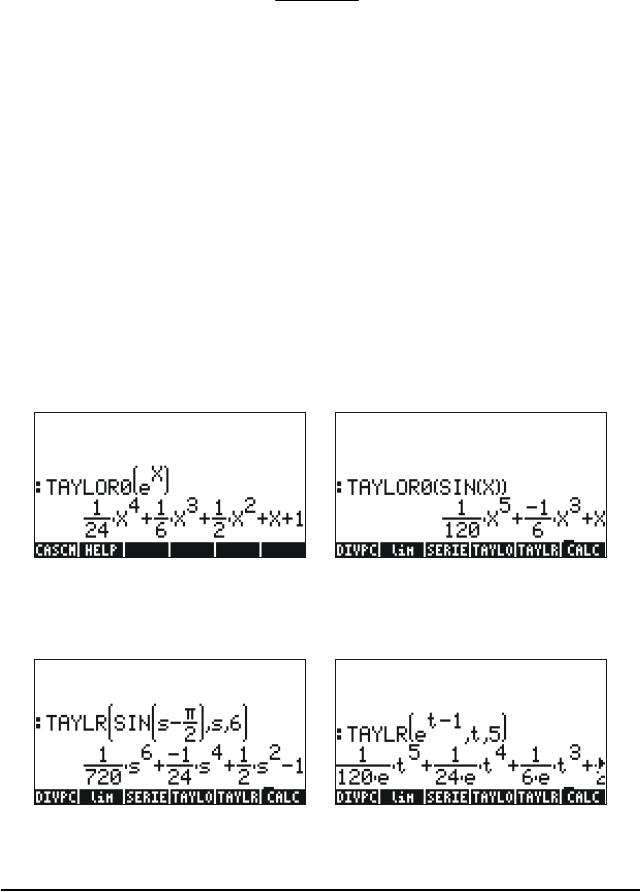
Function TAYLOR0 performs a Maclaurin series expansion, i.e., about X =
0, of an expression in the default independent variable, VX (typically ‘X’).
The expansion uses a 4-th order relative power, i.e., the difference
between the highest and lowest power in the expansion is 4. For example,
Function TAYLR produces a Taylor series expansion of a function of any
variable x about a point x = a for the order k specified by the user. Thus,
the function has the format TAYLR(f(x-a),x,k). For example,
Function SERIES produces a Taylor polynomial using as arguments the
function f(x) to be expanded, a variable name alone (for Maclaurin’s
∑
∞
=
−⋅=
0
)(
)(
!
)(
)(
n
n
o
o
n
xx
n
xf
xf
SG49A.book Page 5 Friday, September 16, 2005 1:31 PM


















