Filter
Top Products
16-12 Step-by-Step Examples
Part 2
Given the equation:
[1]
where the integers x and y are unknown and b
3
and c
3
are defined as in part 1 above:
1. Show that [1] has at least one solution.
2. Apply Euclid’s algorithm to b
3
and c
3
and find a
solution to [1].
3. Find all solutions of [1].
Solution: Equation [1] must have at least one solution,
as it is actually a form of Bézout’s Identity.
In effect, Bézout’s Theorem states that if a and b are
relatively prime, there exists an x and y such that:
Therefore, the equation has at least
one solution.
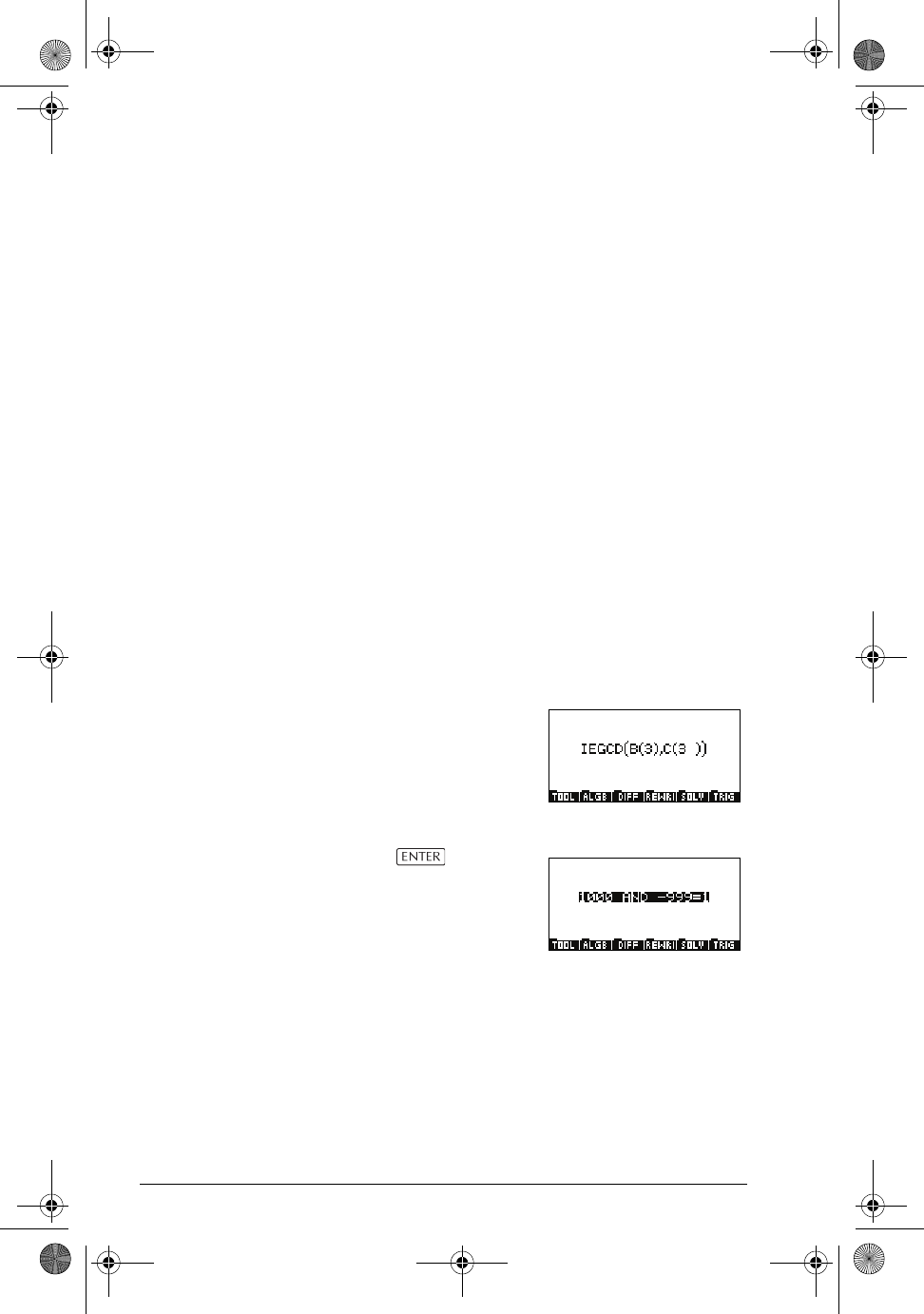
Now enter IEGCD(B(3),
C(3)).
Note that the IEGCD
function can be found on
the INTEGER submenu of
the MATH menu.
Pressing a number
of times returns the result
shown at the right:
In other words:
Therefore, we have a particular solution:
x = 1000, y = –999.
The rest can be done on paper:
,
GCD c
n
b
n
,()GCD c
n
2,()GCD b
n
2,()1===
b
3
xc
3
y 1=⋅+⋅
ax⋅ by⋅+1=
b
3
x⋅ c
3
y⋅+1=
b
3
1000× c
3
999–()×+1=
c
3
b
3
=2+ b
3
999 2 1+×=
hp40g+.book Page 12 Friday, December 9, 2005 1:03 AM