Filter
Top Products
16-26 Step-by-Step Examples
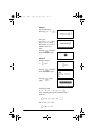
NOTE: The variable VX is now set to N. Reset it to X by
pressing (to display CAS MODES screen)
and change the INDEP VAR setting.
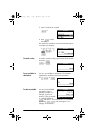
To check the result, we can say that:
and that therefore:
or, simplifying:
If the limit of exists as approaches + in the
inequalities in solution 2 above, we get:
Part 2 1. Show that for every x in [0,2]:
2. Find the value of:
3. Show that for every x in [0,2]:
4. Deduce that:
5. Show that is convergent and find its limit, L.
e
x
1–
x
-------------
x 0→
lim 1=
e
2
n
---
1–
2
n
---
--------------
n +∞→
lim 1=
e
2
n
---
1–
⎝⎠
⎜⎟
⎛⎞
n⋅
n +∞→
lim 2=
Lu
n
n ∞
3
2
---
2⋅ L
7
4
---
2⋅≤≤
2x 3+
x 2+
---------------
2
1
x 2+
------------
–=
I
2x 3+
x 2+
---------------
dx
0
2
∫
=
1 e
x
n
---
e
2
n
---
≤≤
1 u
n
e
2
n
---
I⋅≤≤
u
n
hp40g+.book Page 26 Friday, December 9, 2005 1:03 AM