186 Chapter 11: Differential Equation Graphing
11DIFFEQ.DOC TI-89/TI-92 Plus: Differential Equation (English) Susan Gullord Revised: 02/23/01 11:04 AM Printed: 02/23/01 2:15 PM Page 186 of 26
A system of equations can be defined in various ways, but the
following is a general method.
1. Rewrite the original differential
equation as necessary.
a. Solve for the highest-ordered
derivative.
b. Express it in terms of
y
and
t
.
c. On the right side of the equation
only, substitute to eliminate any
references to derivative values.
In place of: Substitute:
y
y'
y''
y'''
y
(4)
©
y1
y2
y3
y4
y5
©
d. On the left side of the equation,
substitute for the derivative value
as shown below.
In place of: Substitute:
y'
y''
y'''
y
(4)
©
y1'
y2'
y3'
y4'
©
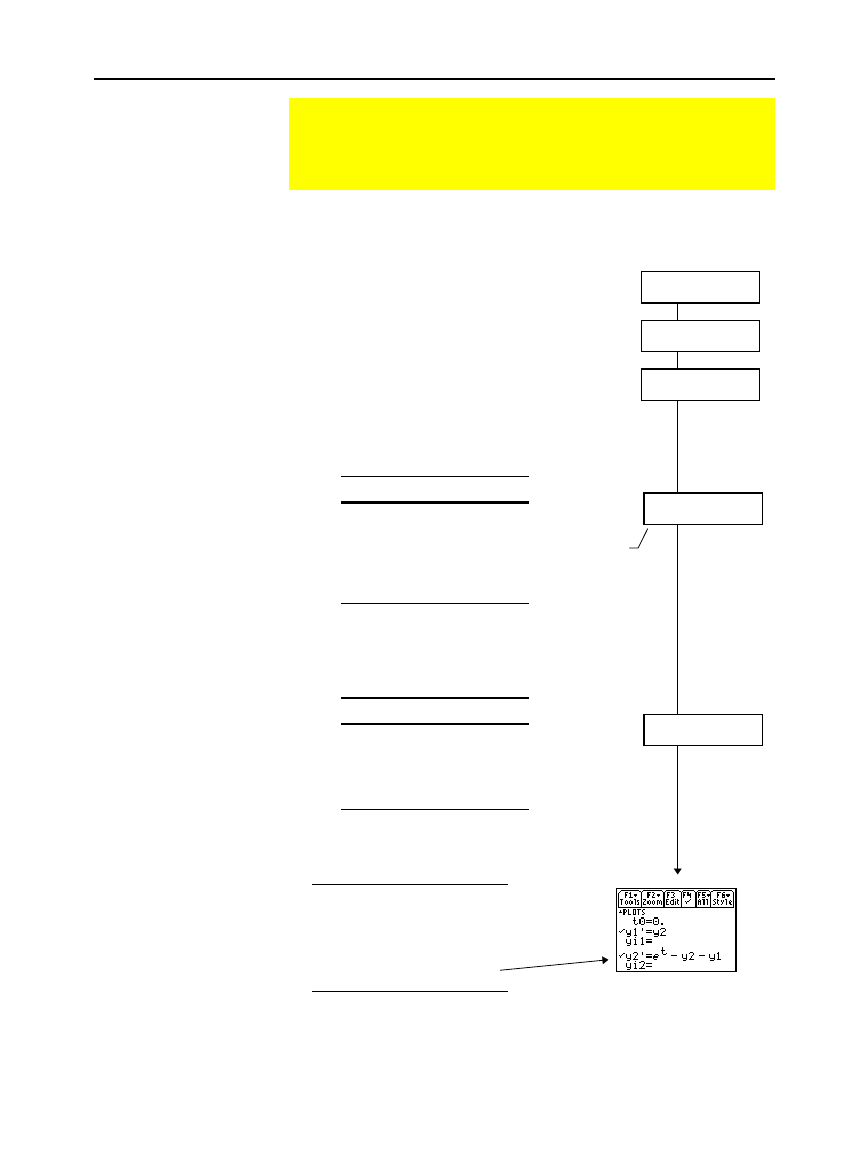
2. On the applicable lines in the Y= Editor,
define the system of equations as:
y1' = y2
y2' = y3
y3' = y4
– up to –
y
n
' =
your n
th
-order equation
In a system such as this, the solution to the
y1'
equation is the
solution to the
n
th
-order equation. You may want to deselect any
other equations in the system.
Defining a System for Higher-Order Equations
In the Y= Editor, you must enter all differential equations as
1st-order equations. If you have an
n
th
-order equation, you
must transform it into a system of
n
1st-order equations.
Transforming an
Equation into a 1st-
Order System
Note:
To produce a 1st-
order equation, the right
side must contain non-
derivative variables only.
Note:
Based on the above
substitutions, the y' lines in
the Y= Editor represent:
y1' = y'
y2' = y''
etc.
So, this example’s 2nd-
order equation is entered on
the y2' line.
Do not
substitute on
the left side
at this time.
y'' + y' + y =
e
x
y'' =
e
x
ì
y'
ì
y
y'' =
e
t
ì
y'
ì
y
y'' =
e
t
ì
y2
ì
y1
y2' =
e
t
ì
y2
ì
y1


















