538 Appendix A: Functions and Instructions
8992APPA.DOC TI-89 / TI-92 Plus: Appendix A (US English) Susan Gullord Revised: 02/23/01 1:48 PM Printed: 02/23/01 2:21 PM Page 538 of 132
x
ê
CATALOG
(^
-1
)
expression1
x
ê
⇒
expression
list1
x
ê
⇒
list
Returns the reciprocal of the argument.
For a list, returns the reciprocals of the
elements in
list1
.
3.1^
ë
1
¸
.322581
{a,4,
ë
.1,x
ì
2}^
ë
1
¸
{
1
a
1
4
ë
10.
1
x
ì
2
}
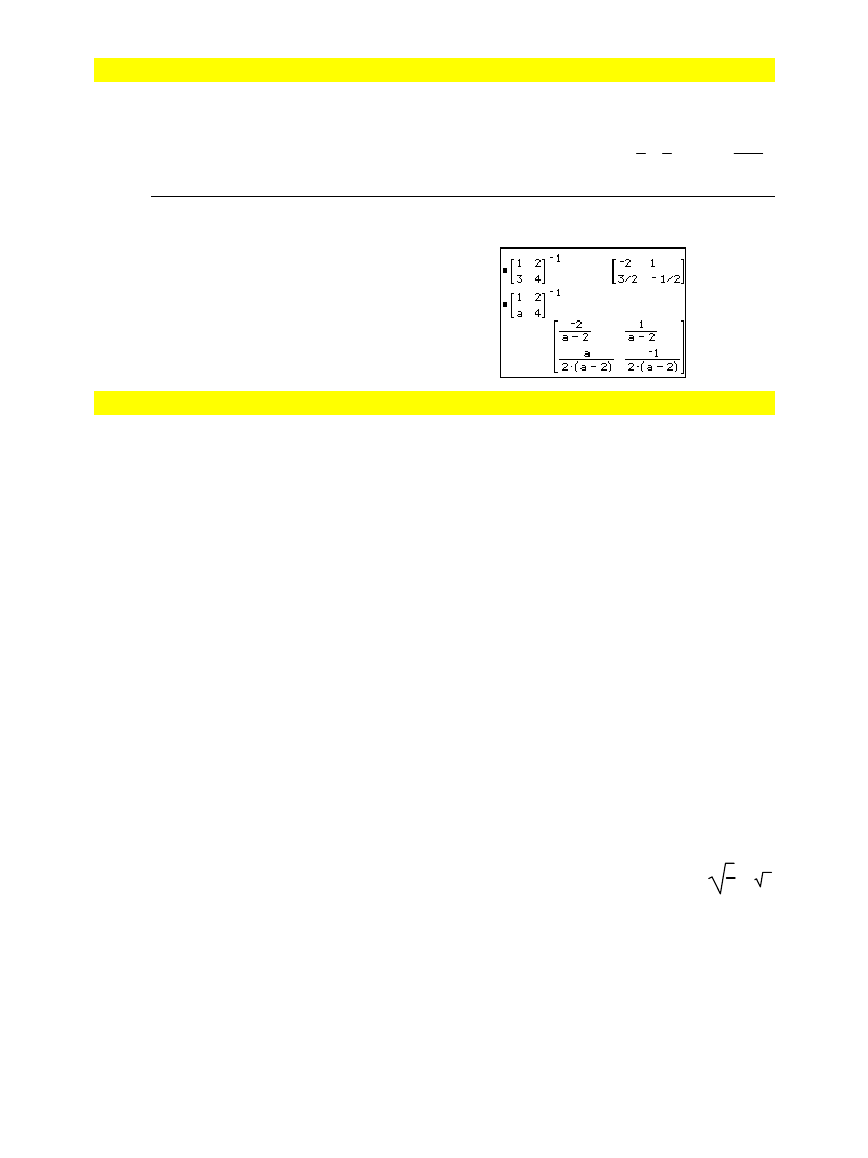
squareMatrix1
x
ê
⇒
squareMatrix
Returns the inverse of
squareMatrix1
.
squareMatrix1
must be a non-singular square
matrix.
[1,2;3,4]^
ë
1
¸
[1,2;a,4]^
ë
1
¸
|
(“with”)
TI
-
89:
Í
key TI
-
92 Plus:
2
Í
key
expression
|
Boolean expression1
[
and Boolean
expression2
]
...
[
and Boolean expressionN
]
The “with” (|) symbol serves as a binary
operator. The operand to the left of | is an
expression. The operand to the right of |
specifies one or more relations that are
intended to affect the simplification of the
expression. Multiple relations after | must be
joined by a logical “and”.
The “with” operator provides three basic
types of functionality: substitutions, interval
constraints, and exclusions.
x+1| x=3
¸
4
x+y| x=sin(y)
¸
sin(y)
+
y
x+y| sin(y)=x
¸
x
+
y
Substitutions are in the form of an equality,
such as
x=3
or
y=sin(x)
. To be most effective,
the left side should be a simple variable.
expression
|
variable
=
value
will substitute
value
for every occurrence of
variable
in
expression
.
x^3
ì
2x+7
!
f(x)
¸
Done
f(x)| x=‡(3)
¸
‡3
+
7
(sin(x))^2+2sin(x)
ì
6
|
sin(x)=d
¸
d
ñ
+2d
ì
6
Interval constraints take the form of one or
more inequalities joined by logical “and”
operators. Interval constraints also permit
simplification that otherwise might be invalid
or not computable.
solve(x^2
ì
1=0,x)
|
x>0 and x<2
¸
x
=
1
‡(x)
ù
‡(1/x)|x>0
¸
1
‡(x)
ù
‡(1/x)
¸
1
x
ø
x
Exclusions use the “not equals” (/= or
ƒ
)
relational operator to exclude a specific
value from consideration. They are used
primarily to exclude an exact solution when
using
cSolve()
,
cZeros()
,
fMax()
,
fMin()
,
solve()
,
zeros()
, etc.
solve(x^2
ì
1=0,x)| xƒ1
¸
x
=
ë
1


















