SR850 BASICS
Lock-in amplifiers are used to detect and measure
very small AC signals - all the way down to a few
nanovolts! Accurate measurements may be made
even when the small signal is obscured by noise
sources many thousands of times larger.
Lock-in amplifiers use a technique known as
phase-sensitive detection to single out the compo-
nent of the signal at a specific reference frequency
AND phase. Noise signals at frequencies other
than the reference frequency are rejected and do
not affect the measurement.
Why use a lock-in?
Let's consider an example. Suppose the signal is a
10 nV sine wave at 10 kHz. Clearly some amplifi-
cation is required. A good low noise amplifier will
have about 5 nV/√Hz of input noise. If the amplifier
bandwidth is 100 kHz and the gain is 1000, then
we can expect our output to be 10 µV of signal
(10 nV x 1000) and 1.6 mV of broadband noise
(5 nV/√Hz x √100 kHz x 1000). We won't have
much luck measuring the output signal unless we
single out the frequency of interest.
If we follow the amplifier with a band pass filter
with a Q=100 (a VERY good filter) centered at
10 kHz, any signal in a 100 Hz bandwidth will be
detected (10 kHz/Q). The noise in the filter pass
band will be 50 µV (5 nV/√Hz x √100 Hz x 1000)
and the signal will still be 10 µV. The output noise
is much greater than the signal and an accurate
measurement can not be made. Further gain will
not help the signal to noise problem.
Now try following the amplifier with a phase-
sensitive detector (PSD). The PSD can detect the
signal at 10 kHz with a bandwidth as narrow as
0.01 Hz! In this case, the noise in the detection
bandwidth will be only 0.5 µV (5 nV/√Hz x √.01 Hz
x 1000) while the signal is still 10 µV. The signal to
noise ratio is now 20 and an accurate measure-
ment of the signal is possible.
What is phase-sensitive detection?
Lock-in measurements require a frequency refer-
ence. Typically an experiment is excited at a fixed
frequency (from an oscillator or function generator)
and the lock-in detects the response from the
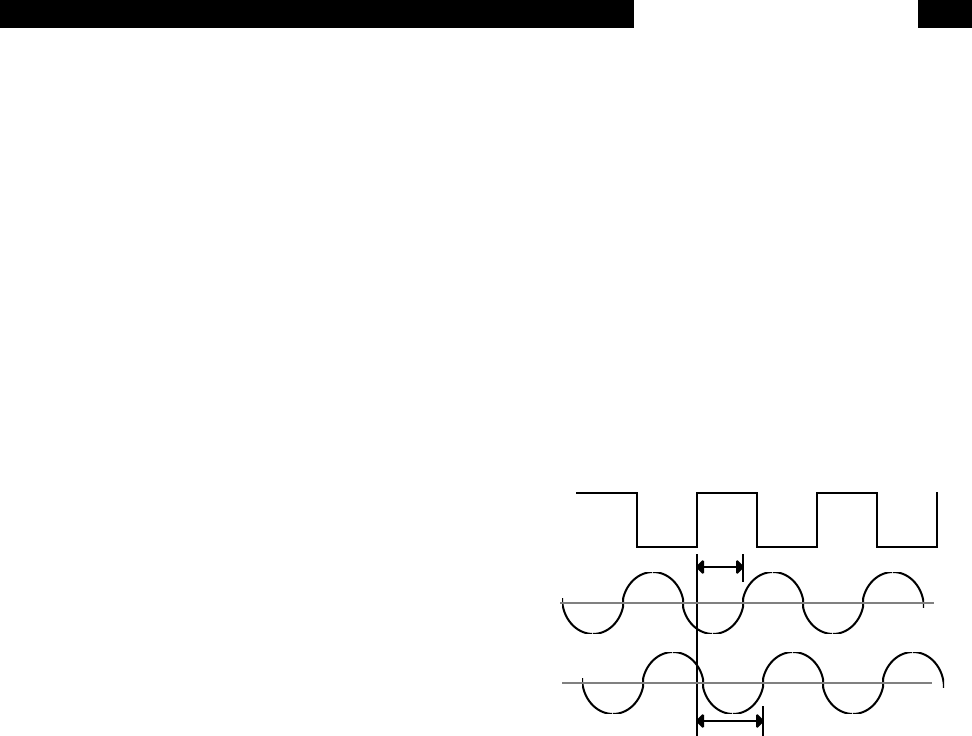
experiment at the reference frequency. In the dia-
gram below, the reference signal is a square wave
at frequency ω
r
. This might be the sync output
from a function generator. If the sine output from
the function generator is used to excite the experi-
ment, the response might be the signal waveform
shown below. The signal is V
sig
sin(ω
r
t + θ
sig
)
where V
sig
is the signal amplitude.
The SR850 generates its own sine wave, shown
as the lock-in reference below. The lock-in refer-
ence is V
L
sin(ω
L
t + θ
ref
).
The SR850 amplifies the signal and then multiplies
it by the lock-in reference using a phase-sensitive
detector or multiplier. The output of the PSD is
simply the product of two sine waves.
V
psd
= V
sig
V
L
sin(ω
r
t + θ
sig
)sin(ω
L
t + θ
ref
)
= 1/2 V
sig
V
L
cos([ω
r
- ω
L
]t + θ
sig
- θ
ref
) -
1/2 V
sig
V
L
cos([ω
r
+ ω
L
]t + θ
sig
+ θ
ref
)
The PSD output is two AC signals, one at the dif-
ference frequency (ω
r
- ω
L
) and the other at the
sum frequency (ω
r
+ ω
L
).
If the PSD output is passed through a low pass
filter, the AC signals are removed. What will be
left? In the general case, nothing. However, if ω
r
equals ω
L
, the difference frequency component
will be a DC signal. In this case, the filtered PSD
output will be
V
psd
= 1/2 V
sig
V
L
cos(θ
sig
- θ
ref
)
WHAT IS A LOCK-IN AMPLIFIER?
3-1
θ
ref
Reference
Signal
Lock-in Reference
sig
θ


















