1-10
4. Input the first letter of the command you want to input. This will display the first command
that starts with that letter.
5. Use the cursor keys (D, A) to highlight the command you want to input, and then press
(INPUT) or U.
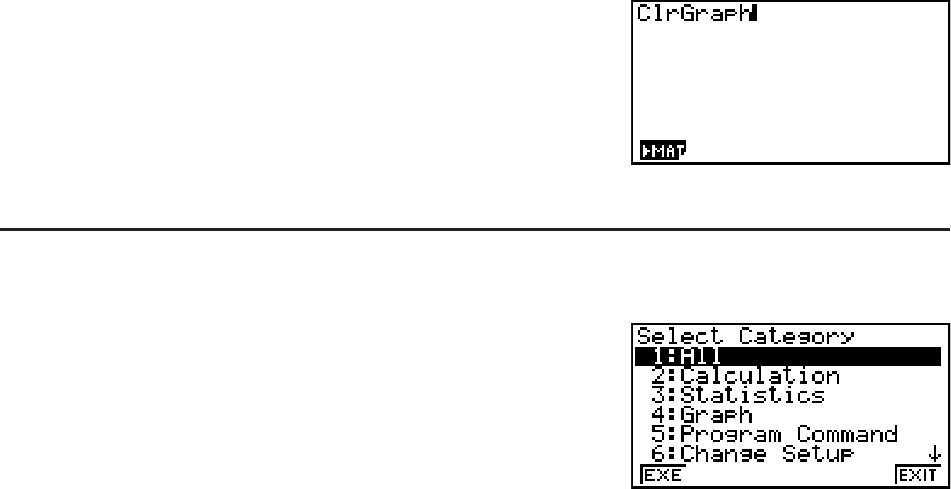
Example To use the Catalog to input the ClrGraph command
C(CATALOG)((C)A~AU
Pressing ) or )(QUIT) closes the Catalog.
S To input a command with ; (fx-9860G Slim only)
1. Press ;.
• This will display the category selection screen.
• (EXE)... {displays a list of commands in the currently selected category}
• (EXIT)... {exits the category selection screen}
2. Continue from step 3 of the procedure under “To use the Catalog to input a command”.
4. Using the Math Input/Output Mode
Important!
• The fx-7400G
ɉ and fx-9750Gɉ are not equipped with a Math input/output mode.
Selecting “Math” for the “Input/Output” mode setting on the Setup screen (page 1-29) turns on
the Math input/output mode, which allows natural input and display of certain functions, just as
they appear in your textbook.
• The operations in this section all are performed in the Math input/output mode.
- The initial default setting for the fx-9860G
ɉ SD/fx-9860Gɉ/fx-9860G AU PLUS is the Math
input/output mode. If you have changed to the Linear input/output mode, switch back to the
Math input/output mode before performing the operations in this section. See “Using the
Setup Screen” (page 1-26) for information about how to switch modes.
- The initial default setting for the fx-9860G Slim/fx-9860G SD/fx-9860G/fx-9860G AU is
the Linear input/output mode. Switch to the Math input/output mode before performing the
operations in this section. See “Using the Setup Screen” (page 1-26) for information about
how to switch modes.
• In the Math input/output mode, all input is insert mode (not overwrite mode) input. Note that
the #(INS) operation (page 1-6) you use in the Linear input/output mode to switch to
insert mode input performs a completely different function in the Math input/output mode. For
more information, see “Using Values and Expressions as Arguments” (page 1-14).
