2-47
• Only square matrices (same number of rows and columns) can be inverted. Trying to invert a
matrix that is not square produces an error.
• A matrix with a determinant of zero cannot be inverted. Trying to invert a matrix with
determinant of zero produces an error.
• Calculation precision is affected for matrices whose determinant is near zero.
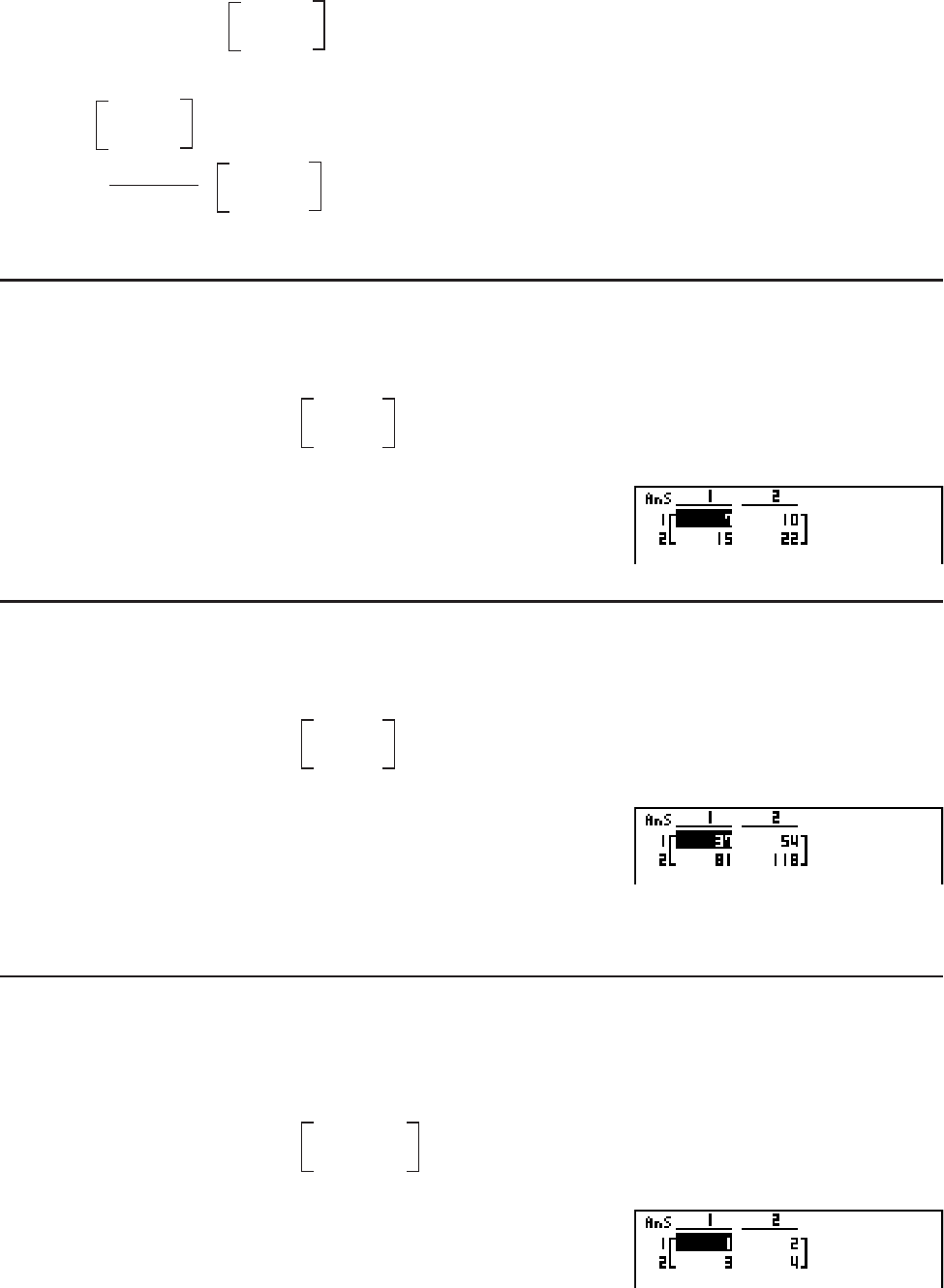
• A matrix being inverted must satisfy the conditions shown below.
AA
–1
= A
–1
A = E =
10
01
The following shows the formula used to invert Matrix A into inverse matrix A
–1
.
A =
ab
cd
A
–1
=
1
ad – bc
d–b
–c a
Note that ad – bc x 0.
S Squaring a Matrix [x
2
]
Example To square the following matrix:
Matrix A =
*(MAT)(Mat)?T(A)VU
S Raising a Matrix to a Power [^]
Example To raise the following matrix to the third power:
Matrix A =
*(MAT)(Mat)?T(A)
,BU
• For matrix power calculations, calculation is possible up to a power of 32766.
S Determining the Absolute Value, Integer Part, Fraction Part, and Maximum
Integer of a Matrix
[OPTN]-[NUM]-[Abs]/[Frac]/[Int]/[Intg]
Example To determine the absolute value of the following matrix:
Matrix A =
*(E)(NUM)(Abs)
*(MAT)(Mat)?T(A)U
12
34
12
34
12
34
12
34
1 –2
–3 4
1 –2
–3 4


















