270
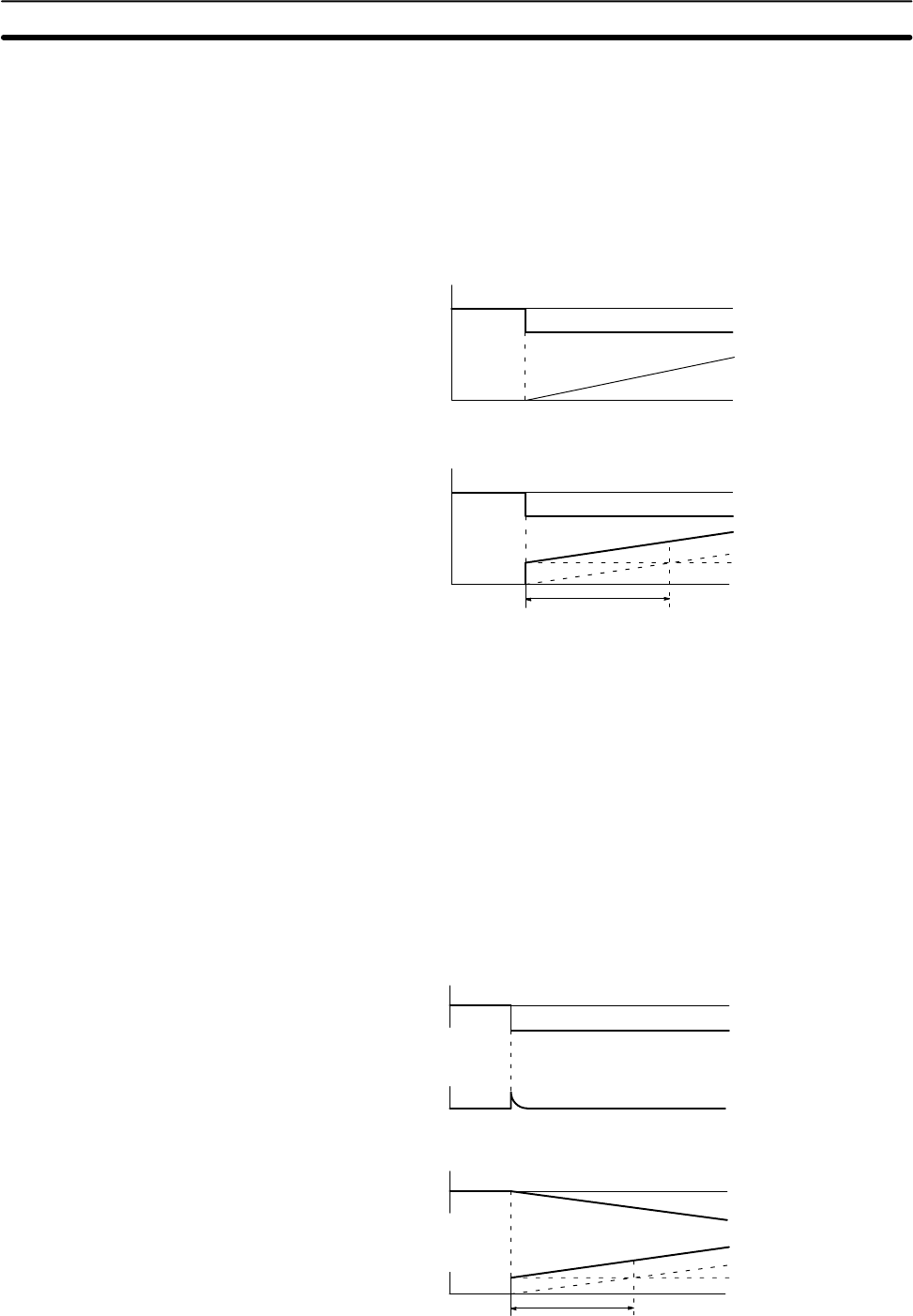
cording to the time that has passed. The strength of the integral operation is indi-
cated by the integral time, which is the time required for the integral operation
amount to reach the same level as the proportional operation amount with re-
spect to the step deviation, as shown in the following illustration. The shorter the
integral time, the stronger the correction by the integral operation will be. If the
integral time is too short, the correction will be too strong and will cause hunting
to occur.
Integral Operation
PI Operation and Integral Time
Deviation
Operation
amount
Step response
PI operation
P operation
Ti: Integral time
0
0
0
0
Deviation
Operation
amount
Step response
I operation
Derivative Operation (D)
Proportional operation and integral operation both make corrections with re-
spect to the control results, so there is inevitably a response delay. Derivative
operation compensates for that drawback. In response to a sudden disturbance
it delivers a large operation amount and rapidly restores the original status. A
correction is executed with the operation amount made proportional to the in-
cline (derivative coefficient) caused by the deviation.
The strength of the derivative operation is indicated by the derivative time, which
is the time required for the derivative operation amount to reach the same level
as the proportional operation amount with respect to the step deviation, as
shown in the following illustration. The longer the derivative time, the stronger
the correction by the derivative operation will be.
Derivative Operation
PD Operation and Derivative Time
Step response
PD operation
P operation
Td: Derivative time
D operation
0
0
0
0
Ramp response
Deviation
Operation
amount
Deviation
Operation
amount
Special Math Instructions Section 5-21
