OVERVIEW OF NUMERIC PROCESSING
handler could determine which element had been accessed, since the operand address field of the
exception pointers would point to the
NaN,
and the
NaN
would contain the index number of the array
element.
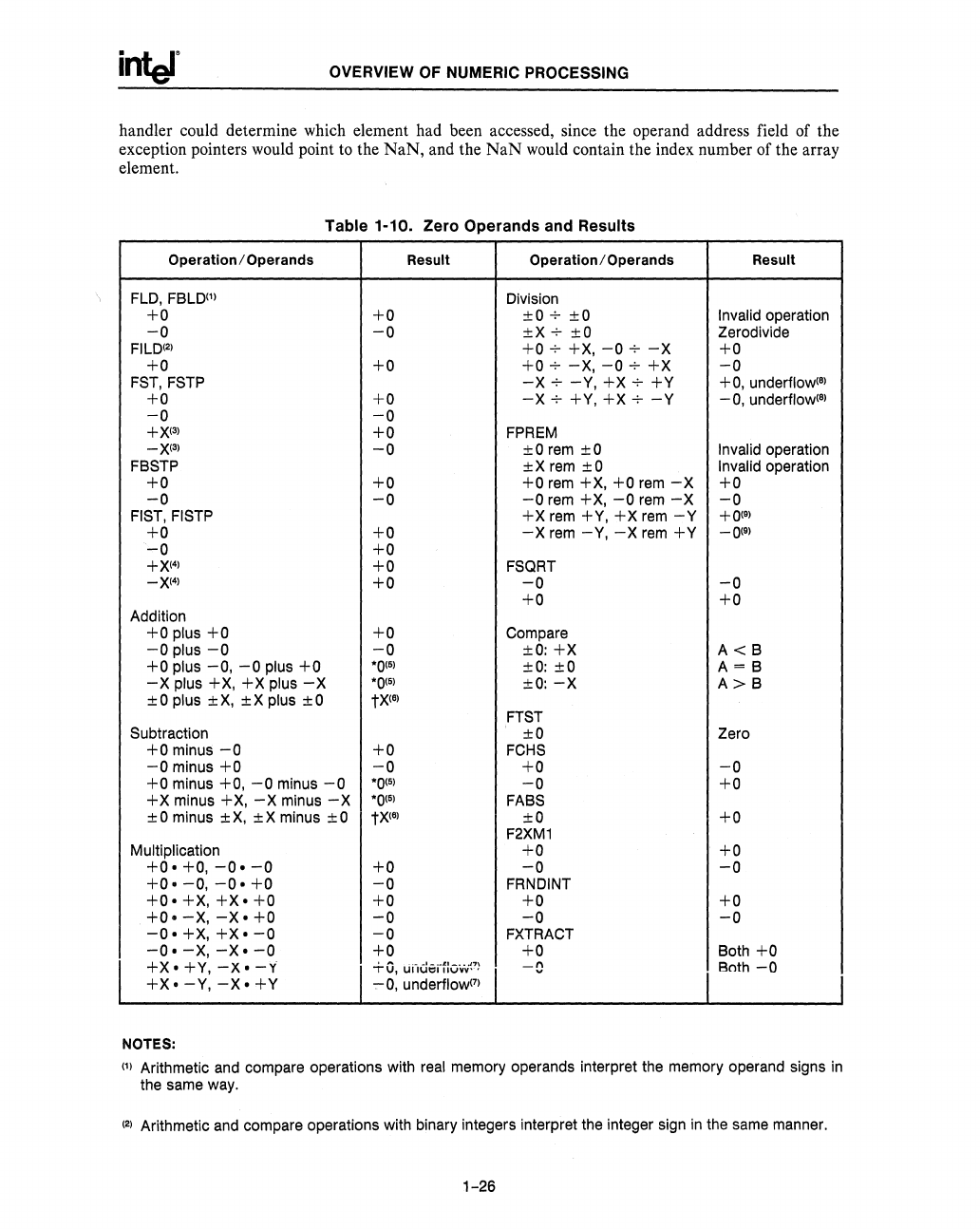
Table 1-10. Zero Operands
and
Results
Operation/Operands Result Operation/ Operands Result
FLD,
FBLD(1)
Division
+0 +0
±o
-;.-
±o
Invalid operation
-0
-0
±X
-;.-
±o
Zerodivide
FILD(2)
+0
-;.-
+X,
-0
-;.-
-X
+0
+0 +0
+0-;.-
-X,
-0-;.-
+X
-0
FST,FSTP
-X
-;.-
-V,
+X
-;.-
+Y
+0,
underflow
lB
)
+0 +0
-X-;.-
+Y,
+X-;.--Y
-0,
underflow
lB
)
-0 -0
+X(3)
+0
FPREM
-X(3)
-0
±O
rem
±O
Invalid operation
FBSTP
±X
rem
±O
Invalid operation
+0 +0
+0
rem
+X,
+0
rem
-X
+0
-0
-0
-0
rem
+X,
-0
rem
-X
-0
FIST,
FISTP
+X
rem
+Y,
+X
rem
-Y
+0
(9
)
+0 +0
-X
rem
-V,
-X
rem
+Y
-0
(9
)
-0
+0
+X(4)
+0
FSQRT
_X(4)
+0
-0
-0
+0
+0
Addition
+0
plus
+0
+0
Compare
-0
plus
-0
-0
±O:
+X
A<B
+0
plus
-0,
-0
plus
+0
'0
(5
)
±o:
±o
A=B
-X
plus
+X,
+X
plus
-X
'0
(5
)
±O:
-X
A>B
±O plus
±X,
±X
plus
±O
tXIB)
FTST
Subtraction
±O
Zero
+0
minus
-0
+0
FCHS
-0
minus
+0
-0
+0
-0
+0
minus
+0,
-0
minus
-0
'0
(5
)
-0
+0
+X
minus +X,
-X
minus
-X
'0
(5
)
FABS
±O minus ±X,
±X
minus
±O
tXI.)
±O
+0
F2XM1
Multiplication
+0
+0
+0·
+0,
-0·-0
+0
-0
-0
+0·
-0,
-0·
+0
-0
FRNDINT
+O·+X,+X·+O
+0 +0
+0
+Oo-X,-X.+O
-0 -0
-0
-0·
+X,
+X·
-0
-0
FXTRACT
-0·
-X,
-X·-O
+0 +0
Both
+0
+X·+Y,-x·-y
+
0,
u(ujcrf:ov·.;!7~
-0
Both
-0
+Xe-Y,-X·+Y
-0,
underflow(7)
NOTES:
I
(1)
Arithmetic
and
compare operations with
real
memory operands interpret
the
memory operand signs
in
the
same
way.
(2)
Arithmetic
and
compare operations with binary integers interpret the integer
sign
in
the
same
manner.
1-26


















