PROGRAMMING NUMERIC APPLICATIONS
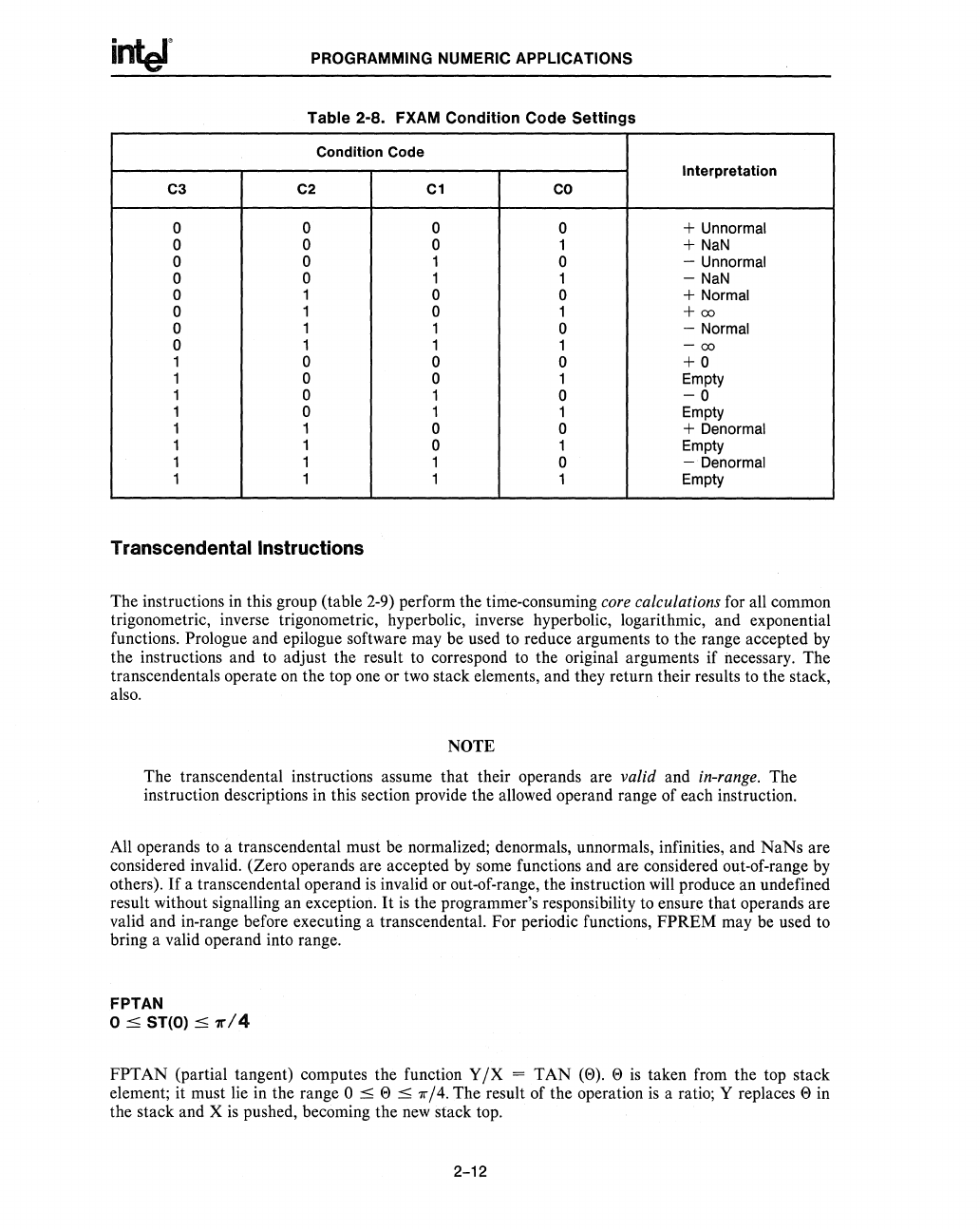
Table
2-8. FXAM
Condition
Code
Settings
Condition Code
Interpretation
C3
C2
C1
CO
0 0 0
0
+
Un
normal
0 0 0 1
+
NaN
0 0
1
0
- Unnormal
0
0
1
1
-
NaN
0
1
0 0 + Normal
0
1 0 1
+00
0
1
1
0
- Normal
0
1 1
1
-
00
1 0
0 0
+0
1 0 0 1 Empty
1 0
1
0
-0
1 0 1 1 Empty
1 1
0 0 +
Denormal
1 1
0 1 Empty
1
1 1
0
-·Denormal
1 1 1 1
Empty
Transcendental Instructions
The
instructions in this group (table 2-9) perform the time-consuming core calculations for all common
trigonometric, inverse trigonometric, hyperbolic, inverse hyperbolic, logarithmic,
and
exponential
functions.
Prologue and epilogue software may be used to reduce arguments to the range accepted by
the instructions and to adjust the result to correspond to the original arguments if necessary.
The
transcendentals operate on the top one
or
two stack elements, and they return their results to the stack,
also.
NOTE
The
transcendental instructions assume
that
their operands are valid and in-range.
The
instruction descriptions in this section provide the allowed operand range
of
each instruction.
All operands to a transcendental must be normalized; denormals, unnormals, infinities, and
NaNs
are
considered invalid. (Zero operands are accepted by some functions and are considered out-of-range by
others).
If
a transcendental operand
is
invalid or out-of-range, the instruction will produce an undefined
result without signalling an exception.
It
is
the programmer's responsibility to ensure
that
operands are
valid and in-range before executing a transcendental. For periodic functions,
FPREM
may be used to
bring a valid operand into range.
FPTAN
o
::;
ST(O) ::;
1r
14
FPTAN
(partial tangent) computes the function Y
IX
=
TAN
(0). 0
is
taken from the top stack
element; it must lie in the range
0 ::; 0 ::;
7r
14.
The
result
of
the operation
is
a ratio; Y replaces 0
in
the stack and X
is
pushed, becoming
the
new stack top.
2-12


















