44 CHAPTER 2. OVERVIEW OF THE UNDERLYING THEORY
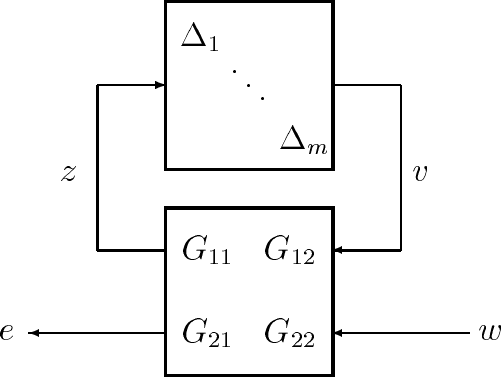
Figure 2.9: Perturbed closed loop system for stability analysis
the induced norms, the reader is referred to Doyle [2]. The major advantage of choosing
BP or BL
2
is that the test for the performance can be considered in terms of the same
norm as stability. This has significant advantages when we are considering performance
and stability in the presence of perturbations, ∆.
2.4.2 Robust Stability and µ
Now we will consider the stability of a closed loop system under perturbations. In
Figure 2.9, G(s), is a perturbation model of a closed loop system. In the following
robust stability and robust performance analyses we will assume that ∆ is linear and
time-invariant.
We will also assume that the interconnection structure G(s) consists of stable transfer
function matrices, where stability is taken to mean that the system has no poles in the
closed right half plane. In practice this amounts to assuming that G
22
(s) (the nominal
closed loop system model) is stable as the other elements, G
11
(s), G
12
(s), and G
21
(s),
are weighting functions and can be chosen to be stable. The nominal closed loop system,
G
22
(s), often arises from a standard design procedure (H
2
, H
∞
, or loopshaping for
example) and will be stable.


















