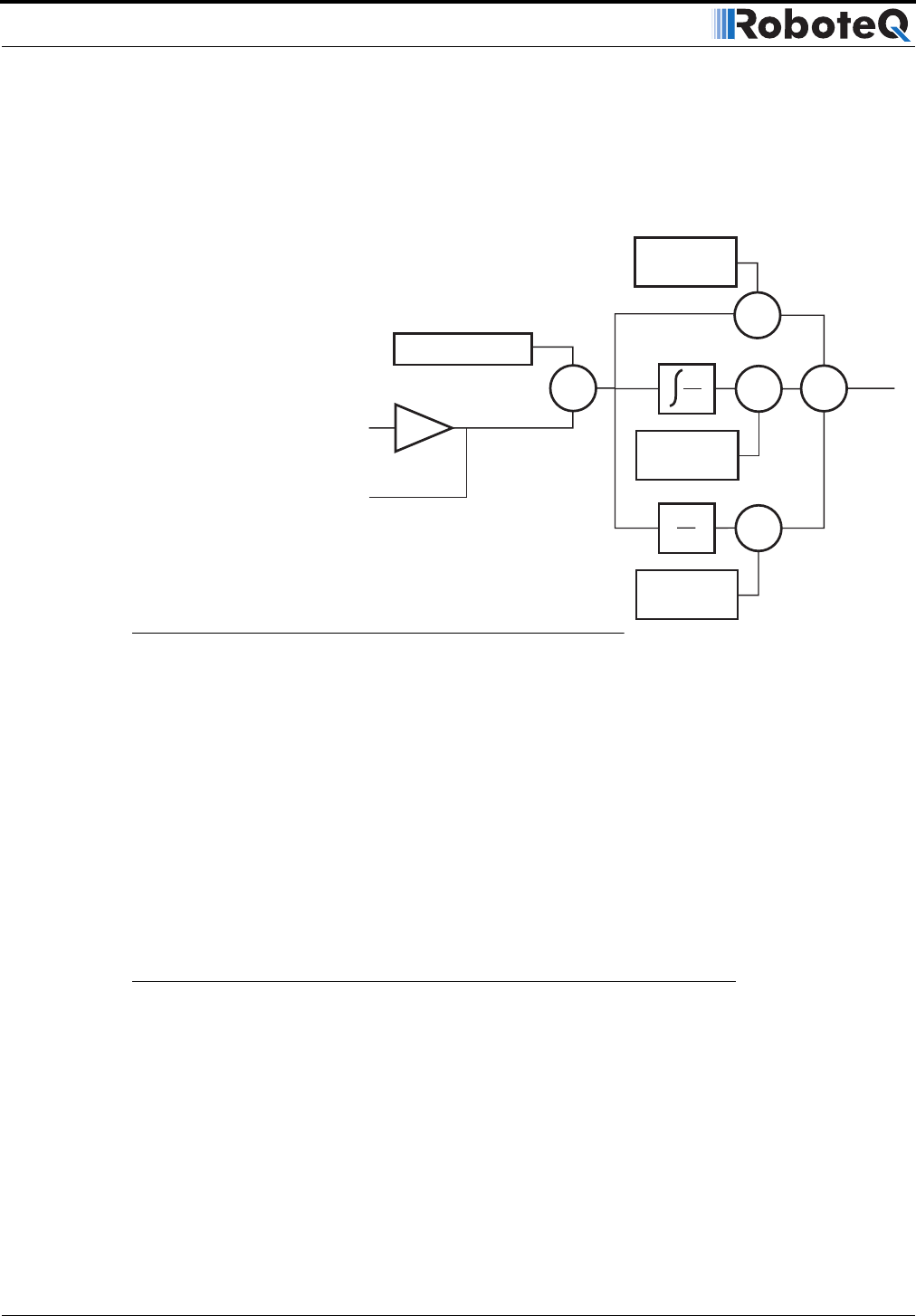
Closed Loop Position Mode
94 AX2550 Motor Controller User’s Manual Version 1.9b. June 1, 2007
A higher Proportional Gain will cause the algorithm to apply a higher level of power for a
given measured error, thus making the motor move quicker. Because of inertia, however, a
faster moving motor will have more difficulty stopping when it reaches its desired position.
It will therefore overshoot and possibly oscillate around that end position.
The Differential component of the algorithm computes the changes to the error from one
16 ms time period to the next. This change will be a relatively large number every time an
abrupt change occurs on the desired position value or the measured position value. The
value of that change is then multiplied by a user-selectable Differential Gain and added to
the output. The effect of this part of the algorithm is to give a boost of extra power when
starting the motor due to changes to the desired position value. The differential component
will also help dampen any overshoot and oscillation.
The Integral component of the algorithm performs a sum of the error over time. In the posi-
tion mode, this component helps the controller reach and maintain the exact desired posi-
tion when the error would otherwise be too small to energize the motor using the
Proportional component alone. Only a very small amount of Integral Gain is typically
required in this mode.
PID tuning in Position Mode
As discussed above, three parameters - Proportional Gain, Integral Gain and Differential
Gain - can be adjusted to tune the position control algorithm. The ultimate goal in a well
tuned PID is a motor that reaches the desired position quickly without overshoot or oscilla-
tion.
Because many mechanical parameters such as motor power, gear ratio, load and inertia are
difficult to model, tuning the PID is essentially a manual process that takes experimenta-
tion.
Desired Position
Differential
Gain
Proportional
Gain
E= Error
Output
Measured Position
Analog Position
Sensor
or
Optical Encoder
A/D
-
x
Σ
x
dE
dt
Integral
Gain
x
dE
dt
FIGURE 61. PID algorithm used in Position mode


















