Vol. 2A 3-359
INSTRUCTION SET REFERENCE, A-M
FPREM—Partial Remainder
FPREM—Partial Remainder
Description
Computes the remainder obtained from dividing the value in the ST(0) register (the
dividend) by the value in the ST(1) register (the divisor or modulus), and stores the
result in ST(0). The remainder represents the following value:
Remainder ← ST(0) − (Q ∗ ST(1))
Here, Q is an integer value that is obtained by truncating the floating-point number
quotient of [ST(0) / ST(1)] toward zero. The sign of the remainder is the same as the
sign of the dividend. The magnitude of the remainder is less than that of the
modulus, unless a partial remainder was computed (as described below).
This instruction produces an exact result; the inexact-result exception does not occur
and the rounding control has no effect. The following table shows the results
obtained when computing the remainder of various classes of numbers, assuming
that underflow does not occur.
When the result is 0, its sign is the same as that of the dividend. When the modulus
is ∞, the result is equal to the value in ST(0).
Opcode Instruction 64-Bit
Mode
Compat/
Leg Mode
Description
D9 F8 FPREM Valid Valid Replace ST(0) with the remainder obtained
from dividing ST(0) by ST(1).
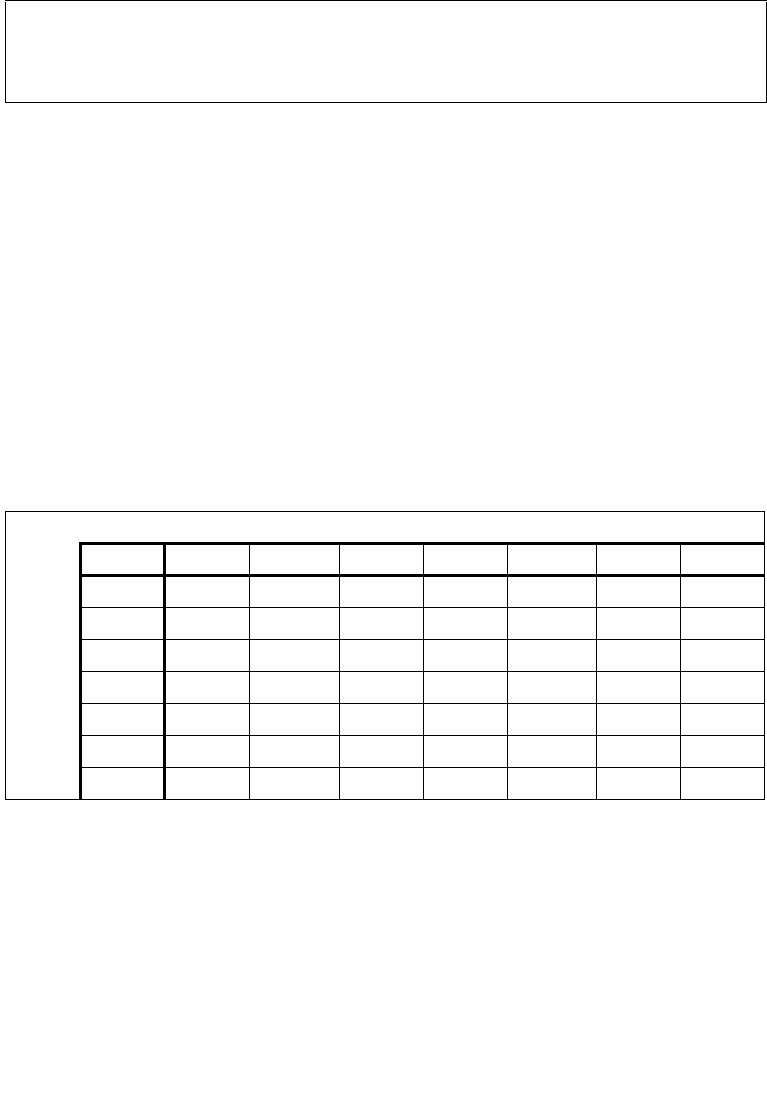
Table 3-36. FPREM Results
ST(1)
−∞ −F −0 +0 +F+∞ NaN
−∞ ******NaN
ST(0) −FST(0)−F or −0** **−F or −0ST(0) NaN
−0 −0 −0**−0 −0NaN
+0 +0 +0**+0 +0NaN
+FST(0)+F or +0** **+F or +0ST(0) NaN
+
∞ ******NaN
NaN NaN NaN NaN NaN NaN NaN NaN
NOTES:
F Means finite floating-point value.
* Indicates floating-point invalid-arithmetic-operand (#IA) exception.
** Indicates floating-point zero-divide (#Z) exception.


















