312 Instruction Latencies Appendix C
25112 Rev. 3.06 September 2005
Software Optimization Guide for AMD64 Processors
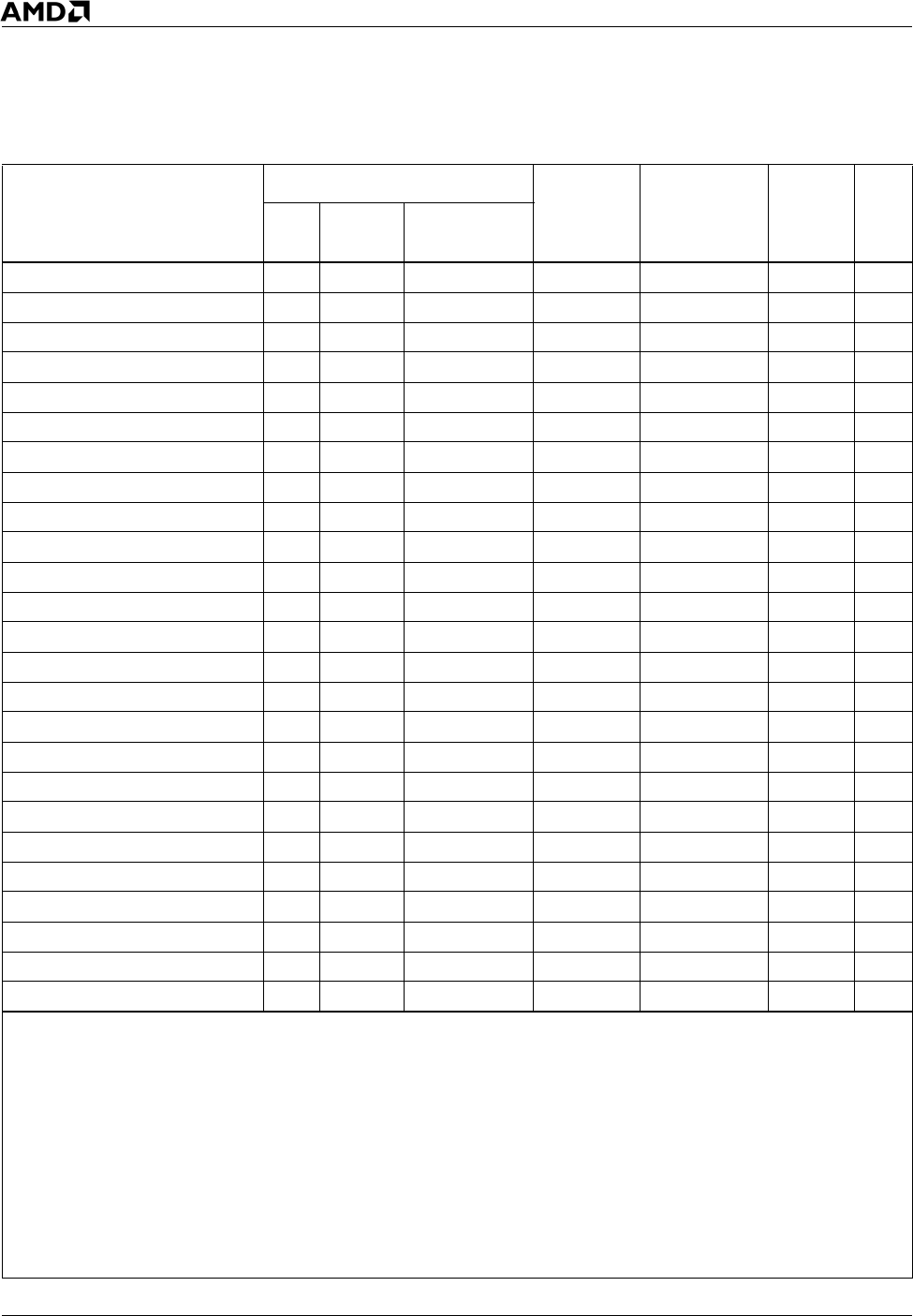
FSTENV [mem28byte] D9h mm-110-xxx VectorPath - 89
FSTP [mem32real] D9h mm-011-xxx DirectPath FADD/FMUL 2
FSTP [mem64real] DDh mm-011-xxx DirectPath FADD/FMUL 2
FSTP [mem80real] D9h mm-111-xxx VectorPath - 8
FSTP ST(i) DDh 11-011-xxx DirectPath FADD/FMUL 2
FSTSW AX DFh 11-100-000 VectorPath - 12
FSTSW [mem16] DDh mm-111-xxx VectorPath FSTORE 8 3
FSUB [mem32real] D8h mm-100-xxx DirectPath FADD 6
FSUB [mem64real] DCh mm-100-xxx DirectPath FADD 6
FSUB ST, ST(i) D8h 11-100-xxx DirectPath FADD 4 1
FSUB ST(i), ST DCh 11-101-xxx DirectPath FADD 4 1
FSUBP ST(i), ST DEh 11-101-xxx DirectPath FADD 4 1
FSUBR [mem32real] D8h mm-101-xxx DirectPath FADD 6
FSUBR [mem64real] DCh mm-101-xxx DirectPath FADD 6
FSUBR ST, ST(i) D8h 11-100-xxx DirectPath FADD 4 1
FSUBR ST(i), ST DCh 11-101-xxx DirectPath FADD 4 1
FSUBRP ST(i), ST DEh 11-100-xxx DirectPath FADD 4 1
FTST D9h 11-100-100 DirectPath FADD 2
FUCOM DDh 11-100-xxx DirectPath FADD 2
FUCOMI ST, ST(i) DBh 11-101-xxx VectorPath FADD 3 3
FUCOMIP ST, ST(i) DFh 11-101-xxx VectorPath FADD 3 3
FUCOMP DDh 11-101-xxx DirectPath FADD 2
FUCOMPP DAh 11-101-001 DirectPath FADD 2
FWAIT 9Bh DirectPath - 0
FXAM D9h 11-100-101 VectorPath - 2
Table 15. x87 Floating-Point Instructions (Continued)
Syntax
Encoding
Decode
type
FPU
pipe(s)
Latency Note
First
byte
Second
byte
ModRM byte
Notes:
1. The last three bits of the ModRM byte select the stack entry ST(i).
2. These instructions have an effective latency as shown. However, these instructions generate an internal NOP
with a latency of two cycles but no related dependencies. These internal NOPs can be executed at a rate of
three per cycle and can use any of the three execution resources.
3. This is a VectorPath decoded operation that uses one execution pipe (one ROP).
4. There is additional latency associated with this instruction. “e” represents the difference between the exponents
of the divisor and the dividend. If “s” is the number of normalization shifts performed on the result, then
n = (s+1)/2 where (0 <= n <= 32).
5. The latency provided for this operation is the best-case latency.
6. The three latency numbers represent the latency values for precision control settings of single precision, double
precision, and extended precision, respectively.


















