10-2 Matrices
8310MTRX.DOC TI-83 international English Bob Fedorisko Revised: 02/19/01 12:35 PM Printed: 02/19/01 1:36
PM Page 2 of 16
Getting Started is a fast-paced introduction. Read the chapter for details.
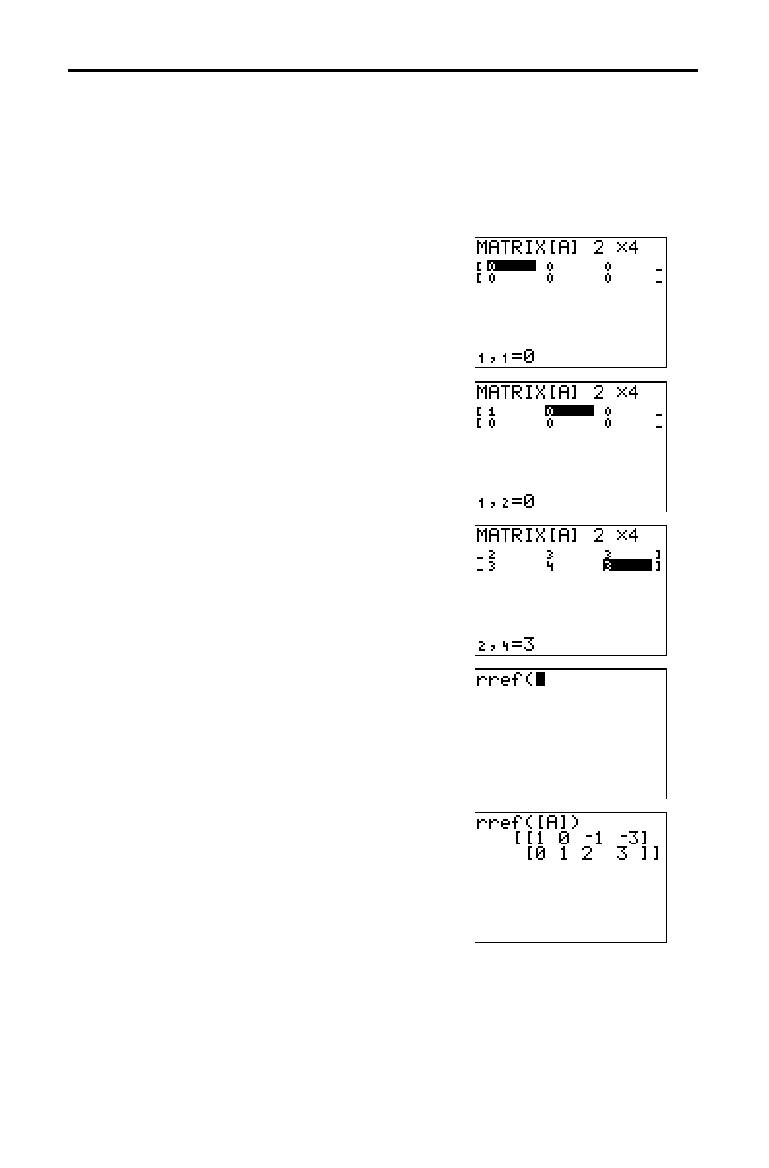
Find the solution of X + 2Y + 3Z = 3 and 2X + 3Y + 4Z = 3. On the TI
-
83, you
can solve a system of linear equations by entering the coefficients as elements
in a matrix, and then using
rref( to obtain the reduced row-echelon form.
1. Press
. Press
~
~
to display the
MATRX EDIT
menu. Press 1 to select 1: [A]¸
2. Press
2
Í
4
Í
to define a 2×4
matrix. The rectangular cursor indicates
the current element. Ellipses (
...) indicate
additional columns beyond the screen.
3. Press 1
Í
to enter the first element.
The rectangular cursor moves to the
second column of the first row.
4. Press 2
Í
3
Í
3
Í
to complete
the first row for X + 2Y + 3Z = 3.
5. Press
2
Í
3
Í
4
Í
3
Í
to
enter the second row for 2X + 3Y + 4Z = 3.
6. Press
y
[
QUIT
] to return to the home
screen. If necessary, press
‘
to clear
the home screen. Press
~
to
display the
MATRX MATH
menu. Press
}
to
wrap to the end of the menu. Select
B:rref(
to copy rref( to the home screen.
7. Press
1 to select 1: [A] from the
MATRX NAMES
menu. Press
¤
Í
. The
reduced row-echelon form of the matrix is
displayed and stored in
Ans.
1X
N
1Z =
L
3 so X =
L
3 + Z
1Y + 2Z = 3 so Y = 3
N
2Z
Getting Started: Systems of Linear Equations


















