878 Appendix A: Functions and Instructions
sinhê(
squareMatrix1
) ⇒
⇒⇒
⇒
squareMatrix
Returns the matrix inverse hyperbolic sine of
squareMatrix1
. This is
not
the same as calculating
the inverse hyperbolic sine of each element. For
information about the calculation method, refer
to
cos().
squareMatrix1
must be diagonalizable. The result
always contains floating-point numbers.
In Radian angle mode:
sinh
ê([1,5,3;4,2,1;6,ë2,1]) ¸
.041… 2.155… 1.158…
1.463… .926… .112…
2.750…
ë 1.528… .572…
SinReg MATH/Statistics/Regressions menu
SinReg
list1
,
list2
[ , [
iterations
] , [
period
] [,
list3
,
list4
] ]
Calculates the sinusoidal regression and updates
all the system statistics variables.
All the lists must have equal dimensions except
for
list4
.
list1
represents xlist.
list2
represents ylist.
list3
represents category codes.
list4
represents category include list.
iterations
specifies the maximum number of times
(1 through 16) a solution will be attempted. If
omitted, 8 is used. Typically, larger values result
in better accuracy but longer execution times, and
vice versa.
period
specifies an estimated period. If omitted,
the difference between values in
list1
should be
equal and in sequential order. If you specify
period
, the differences between x values can be
unequal.
Note:
list1
through
list3
must be a variable name
or c1–c99 (columns in the last data variable
shown in the Data/Matrix Editor).
list4
does not
have to be a variable name and cannot be c1–
c99.
The output of
SinReg is always in radians,
regardless of the angle mode setting.
In function graphing mode:
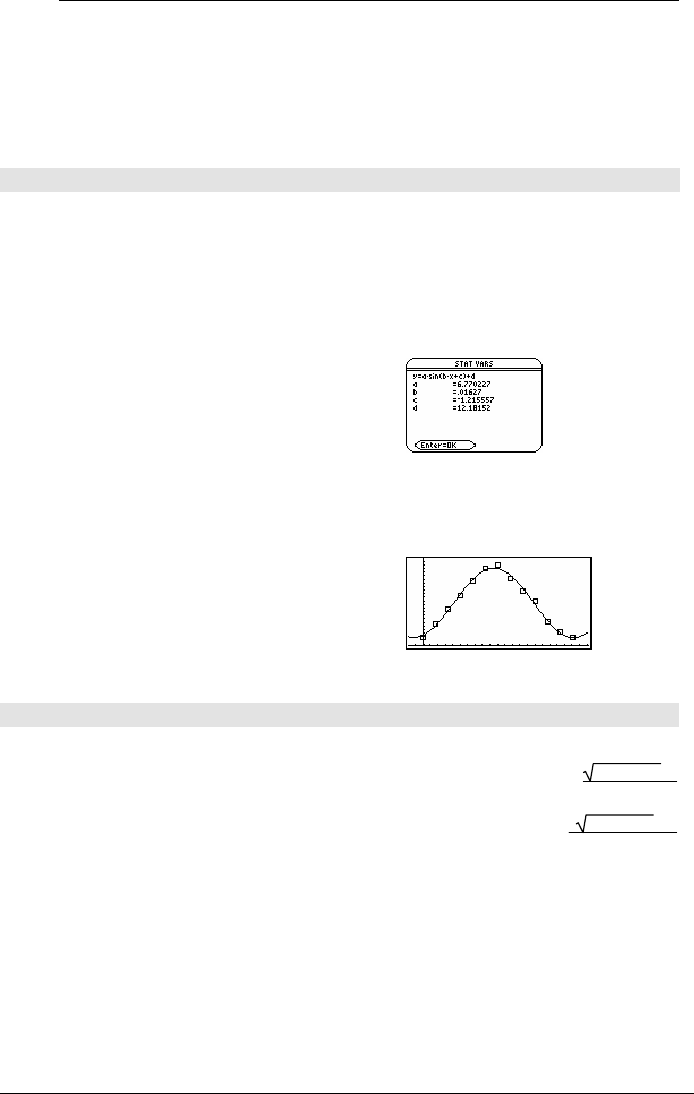
seq(x,x,1,361,30)!L1 ¸
{1 31 61 …}
{5.5,8,11,13.5,16.5,19,19.5,17,
14.5,12.5,8.5,6.5,5.5}
!L2 ¸
{5.5 8 11 …}
SinReg L1,L2
¸ Done
ShowStat
¸
¸
regeq(x)
!y1(x) ¸ Done
NewPlot 1,1,L1,L2
¸ Done
¥%
„9
solve() MATH/Algebra menu
solve(
equation
,
var
) ⇒
⇒⇒
⇒
Boolean expression
solve(
inequality
,
var
) ⇒
⇒⇒
⇒
Boolean expression
Returns candidate real solutions of an equation or
an inequality for
var
. The goal is to return candidates
for all solutions. However, there might be equations
or inequalities for which the number of solutions is
infinite.
solve(aù x^2+bùx+c=0,x) ¸
x
=
bñ -4øaøc-b
2
ø a
or x
=
ë
( bñ -4øaøc+b)
2
ø a
Solution candidates might not be real finite
solutions for some combinations of values for
undefined variables.
ans(1)| a=1 and b=1 and c=1
¸
Error: Non-real result
For the AUTO setting of the Exact/Approx mode,
the goal is to produce exact solutions when they are
concise, and supplemented by iterative searches
with approximate arithmetic when exact solutions
are impractical.
solve((xì a)
e
^(x)=ë xù(xìa),x) ¸
x
= a or x =ë.567...


















