Appendix A: Functions and Instructions 907
&
(append)
¥ p key
string1
&
string2
⇒
⇒⇒
⇒
string
Returns a text string that is
string2
appended to
string1
.
"Hello " & "Nick" ¸
"Hello Nick"
‰
‰‰
‰()
(integrate)
2<key
‰
‰‰
‰(
expression1
,
var
[,
lower
] [,
upper
]) ⇒
⇒⇒
⇒
expression
‰
‰‰
‰(
list1,var
[,
order
]) ⇒
⇒⇒
⇒
list
‰
‰‰
‰(
matrix1,var
[,
order
]) ⇒
⇒⇒
⇒
matrix
Returns the integral of
expression1
with respect to
the variable
var
from
lower
to
upper
.
‰(x^2,x,a,b) ¸
b
ò
3
-
aò
3
Returns an anti-derivative if
lower
and
upper
are
omitted. A symbolic constant of integration such
as
C is omitted.
However,
lower
is added as a constant of
integration if only
upper
is omitted.
‰(x^2,x) ¸
x
ò
3
‰(aùx^2,x,c) ¸
a
ø xò
3
+ c
Equally valid anti-derivatives might differ by a
numeric constant. Such a constant might be
disguised—particularly when an anti-derivative
contains logarithms or inverse trigonometric
functions. Moreover, piecewise constant
expressions are sometimes added to make an
anti-derivative valid over a larger interval than
the usual formula.
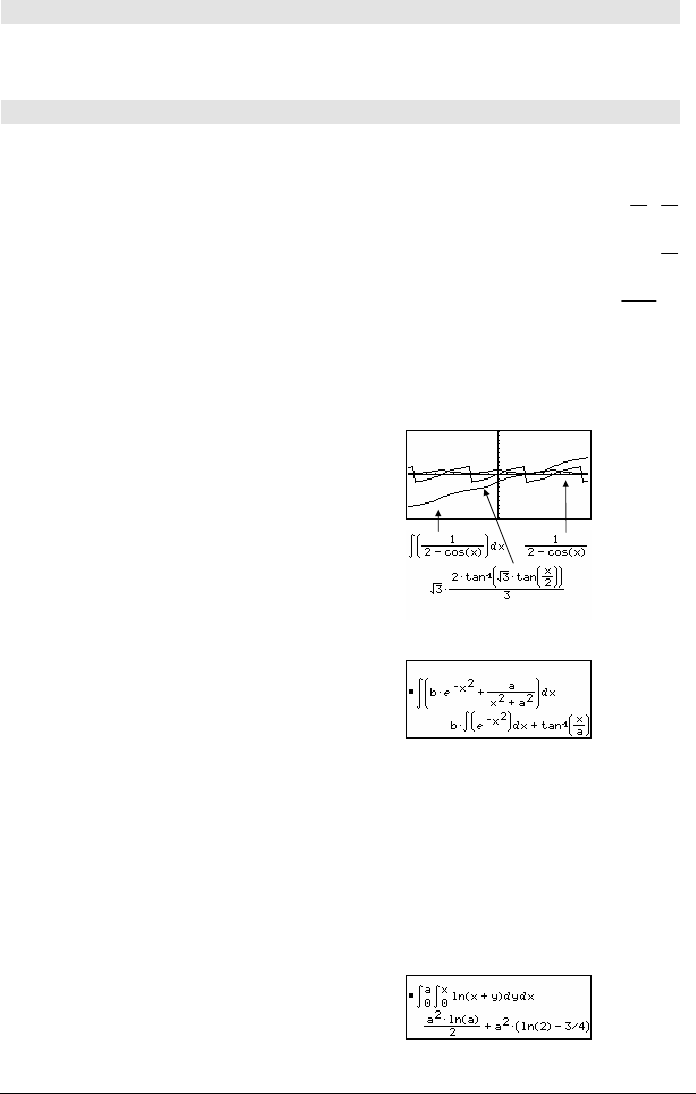
‰(1/(2ìcos(x)),x)! tmp(x) ¸
ClrGraph:Graph tmp(x):Graph
1/(2
ì cos(x)):Graph ‡(3)
(2tan
ê (‡(3)(tan(x/2)))/3) ¸
‰() returns itself for pieces of
expression1
that it
cannot determine as an explicit finite
combination of its built-in functions and
operators.
When
lower
and
upper
are both present, an
attempt is made to locate any discontinuities or
discontinuous derivatives in the interval
lower <
var < upper
and to subdivide the interval at those
places.
‰(bù
e
^(ë x^2)+a/(x^2+a^2),x) ¸
For the AUTO setting of the Exact/Approx mode,
numerical integration is used where applicable
when an anti-derivative or a limit cannot be
determined.
For the APPROX setting, numerical integration is
tried first, if applicable. Anti-derivatives are
sought only where such numerical integration is
inapplicable or fails.
‰(
e
^(ë x^2),x,ë1,1)¥¸ 1.493...
‰() can be nested to do multiple integrals.
Integration limits can depend on integration
variables outside them.
Note: See also
nInt().
‰(‰(ln(x+y),y,0,x),x,0,a) ¸


















